Программа моделирования кривых линий и поверхностей высокого качества по критериям плавности. Приложение AutoCAD.
Методика корректного моделирования NURBS поверхностей Программой


Пример показывает методику исправления конфигурации s-многогранника NURBS поверхности. Методика реализует в Программе теоретические результаты, полученные в статье: Муфтеев В.Г., Романюк А.Н., Марданов А.Р., Фархутдинов И.М. Геометрически устойчивое моделирование NURBS кривых и поверхностей произвольных степеней. 

Моделируемая поверхность задана граничными NURBS кривыми (рис. 7). Для левой и правой граничной линий построены графики кривизны и центров кривизны. Левая NURBS кривая 6-ой степени получена точной аппроксимацией дуги окружности и скорректирована так, что верхняя часть выходит на нулевую кривизну. Правая NURBS кривая 6-ой степени точно моделирует дугу окружности. Нижняя NURBS кривая точно моделирует прямолинейный отрезок. Верхняя NURBS кривая представляет s-образную кривую. Конфигурация проекции отсека поверхности типична для носовой части судна. Размеры и типы граничных NURBS кривых согласованы.




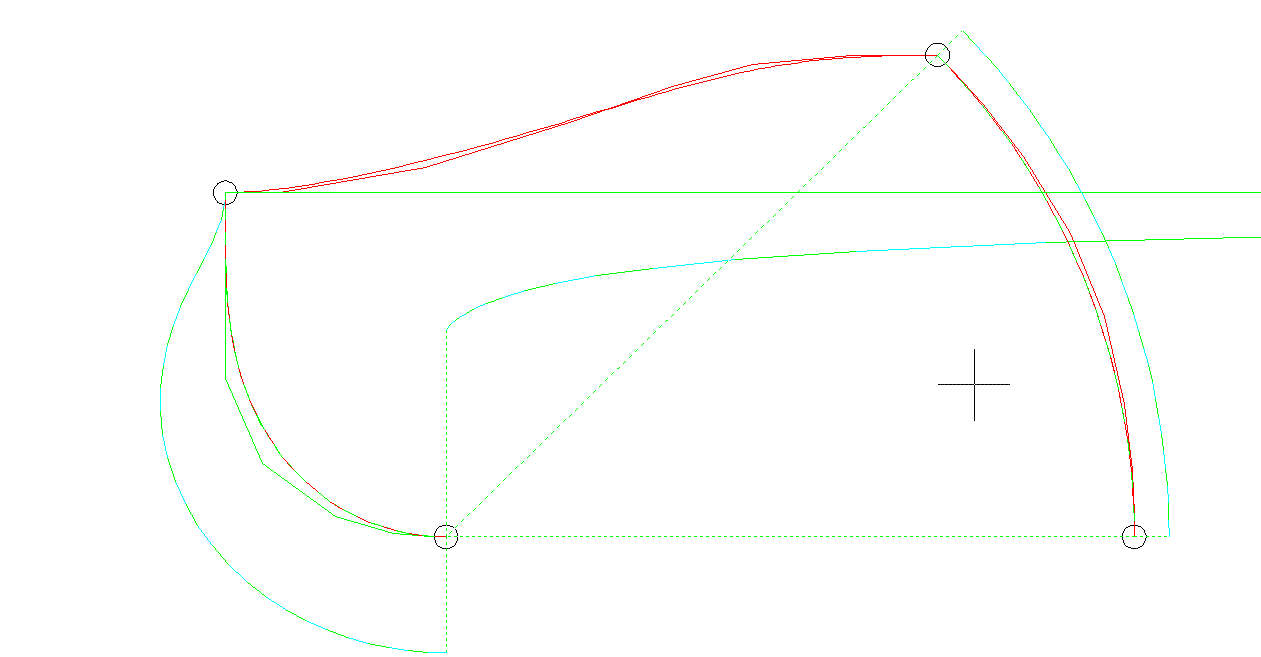
Рис. 7. Граничные линии отсека поверхности с графиками кривизны и центров кривизны

Определим s-многогранник NURBS поверхности по s-полигонам граничных NURBS кривых по формуле Кунса командами V_Model > (выберем кривую) CrvSrf > ToEdge (выберем остальные 3 кривые) (рис. 8).




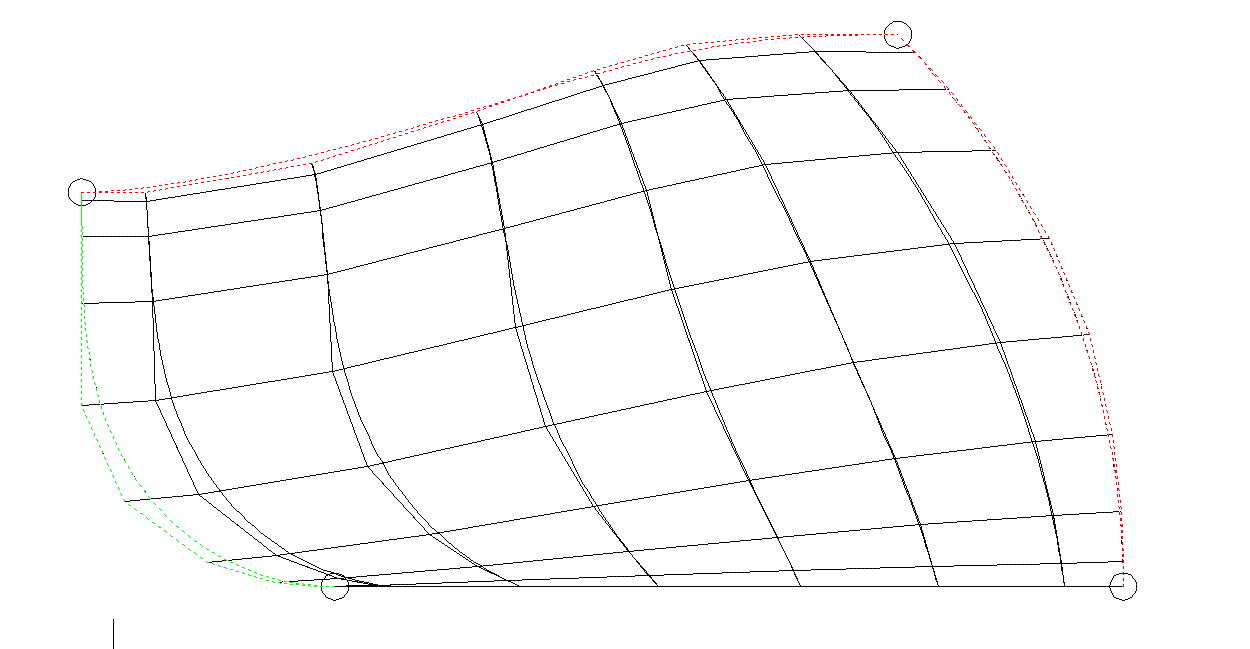
Рис. 8. S-многогранник NURBS поверхности, определенный по s-полигонам граничных NURBS кривых по формуле Кунса

Исследуем качество поверхности командой ViewSurf (рис. 9). Изопараметрические линии поверхности на проекции имеют выраженную осцилляцию формы.





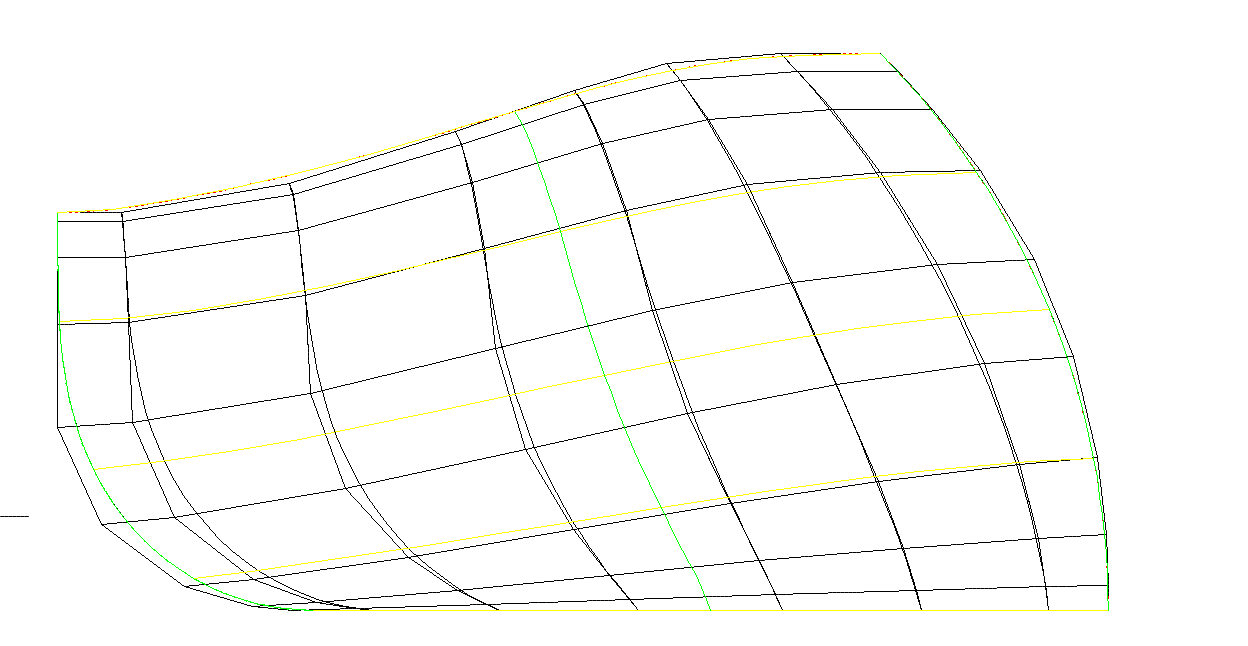
Рис. 9. Осцилляция формы изопараметрической линии – границы аналитических участков NURBS поверхности.

Транспонируем (команда Transpon) геометрический определитель NURBS поверхности (рис. 10). Перейдем к каркасу направляющих (команда Vretcrvs) и отредактируем направляющие NURBS кривые (команда Edtcrvs) vтранспонированной поверхности (см. рис. 11) таким образом, что при фиксированном v = v1, соответствующем линии стыка аналитических отсеков, узловые точки направляющих NURBS кривых будут лежать на одной прямой.




Рис. 10. Отредактированный s-многогранник NURBS поверхности

Исследуем качество поверхности после спрямления изопараметрической линии поверхности по интерполяционному каркасу изопараметрических линий по v (рис. 11).
Прямолинейная изпараметрическая кривая четко делит поверхность на две области с разной формой проекций изопараметрических линий по v.




Рис. 11. Два семейства изопараметрических линий разной формы, разделенные нейтральной прямолинейной изопараметрической линией.

После исправления s-многогранника на плоской проекции интерполированная сеть точек имеет вполне определенную форму без нежелательной осцилляции изопараметрических линий поверхности (рис. 12).




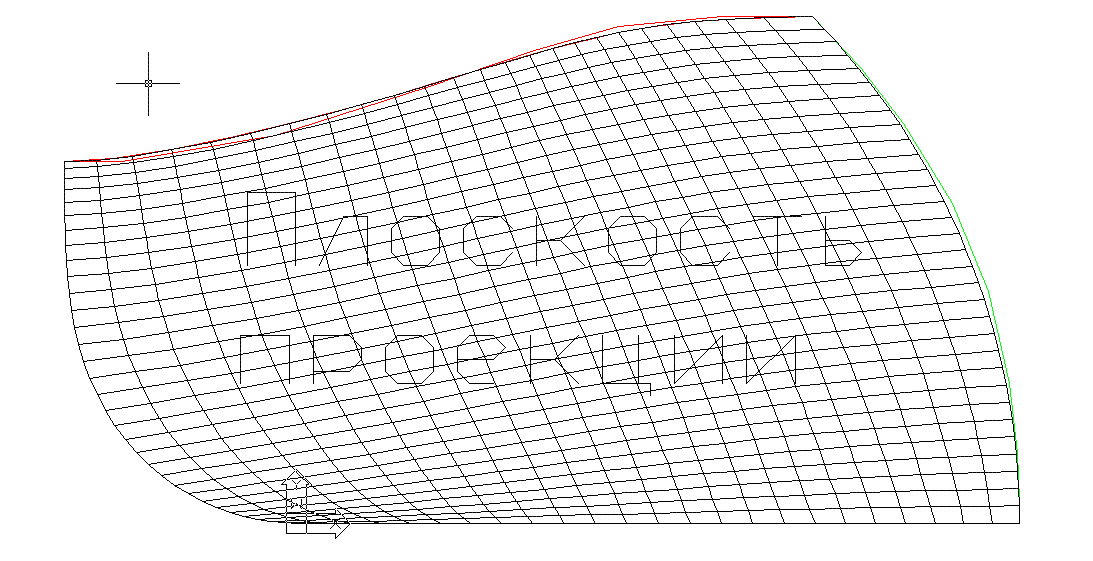
Рис. 12. Интерполяционная сеть точек NURBS поверхности

Одна из возможных пространственных форм поверхности, определенной на данной проекции граничных линий, может быть получена s-многогранником с плоскими направляющими линиями (рис. 14). Координаты точек с весовыми коэффициентами s-многогранника приведены в приложении П4.




Рис. 13. Одна из возможных пространственных форм поверхности, определенной на данной проекции граничных линий.

Исследуем качество данной пространственной NURBS поверхности по форме границ зон знакопостоянства Гауссова кривизны (команда ViewSurf > Indsign > Gausscvt). Благодаря достаточно высоким степеням (6,6) NURBS поверхности, границы зон знакопостоянства Гауссова кривизны представляют плавные кривые линии (рис. 14).




Рис. 14. NURBS поверхность с исправленным s-многогранником. Зоны распределения знака Гауссова кривизны.

Для сравнения на пространственном четырехугольнике граничных NURBS кривых построена поверхность штатной командой AutoCAD _loft.
В контрольном плоском сечении loft поверхности, соответствующем положению прямолинейной образующей исправленного s-многогранника NURBS поверхности, линия сечения имеет выраженную осцилляцию формы (рис. 16).




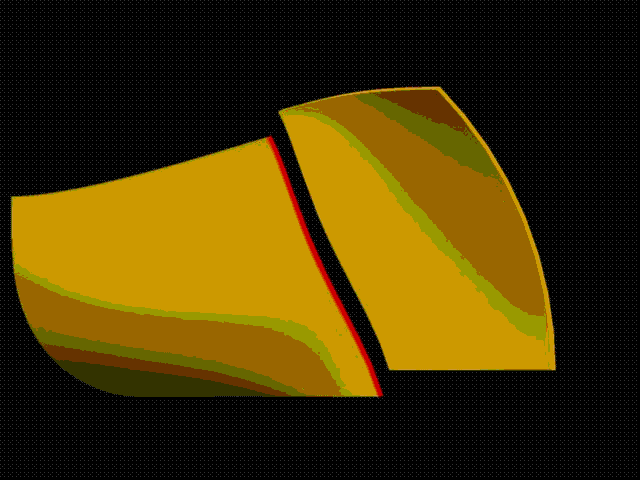
Рис. 15. Контрольное плоское сечение loft поверхности.

Исследуем качество поверхности по известному методу фирмы Daimler Benz. В этом методе качество поверхности исследуется по форме отражения прямолинейных светящихся отрезков.
Для исследования качества поверхностей по методу отражения построена плоская поверхность с материалом “Отделка. Полы. Плитка квадратная”. На исследуемые поверхности наложен материал “Металлы. Металлические несущие каркасы. Сталь” с шаблоном “Улучшенное тонирование металла”. Результаты тонирования исследуемых поверхностей показы на рис. 16, 17.




Рис. 16. Loft поверхность. Отражение “кафельного пола”.




Рис. 17. NURBS поверхность с исправленным s-многогранником. Отражение “кафельного пола”.


Отраженные линии на NURBS поверхности выглядят более “гармоничными”.