Оглавление
1.
Геометрические определители
3.
Установка и вызов и Приложения:
5.
Редактирование кривой на дуальных ГО
6.
Особенности редактирования с фиксацией касательных
7.
Прямое построение кривых на ГО Эрмита.
8.
Улучшение традиционных сплайнов
11.
Правила построения плавных кривых
12.
Сравнение с кривыми класса A
Прикладная библиотека FairCurveModeler_2D версии 2024.11 для
моделирования кривых линий высокого качества в КОМПАС ГРАФИК
Муфтеев В.Г., Зиганшина Ф.Т., Гумеров
В.И.
Аннотация
В
статье описывается приложение КОМПАС ГРАФИК FairCurveModeler_2D.rtw для моделирования кривых линий высокого качества (класса
F), разработанное на основе функционала C3D FairCurveModeler.
Кратко описывается команды приложения.
Предлагается способ редактирования кривой на дуальных
видах геометрического определителя в качестве улучшения команды “Метасплайн” в
КОМПАС 3D.
Предлагается способ улучшения метода построения B-сплайновых кривых на узловых точках с помощью опции
гармонизации ломаной на V-кривой.
Показываются возможности построения и редактирования
кривых с обеспечением фиксации касательных в точках исходной ломаной.
Предлагается использовать метод прямого моделирования
и редактирования на ГО Эрмита для 1) моделирования и гибкого редактирования
кривых произвольной формы и 2) высококачественной аппроксимации аналитических
кривых.
Проводится сравнительный анализ методов построения
кривых класса A в NX и кривых класса F в C3D FairCurveModeler. Показывается преимущество методов C3D FairCurveModeler перед методами моделирования кривых класса A в NX Spline Studio.
Приложение может использоваться и в документах 3D для пространственного моделирования процедурных
поверхностей при подготовке эскизов кривых высокого качества.
Введение
В
настоящее время актуальным является повышение качества технических изделий с
функциональными кривыми и поверхностями. Качество функциональных кривых и
поверхностей является определяющим для проектных характеристик таких изделий.
Особенно это важно в наукоемких и высокотехнологичных отраслях (в авиастроении,
судостроении, авиа-двигателестроении, автопроме, турбостроении), где качество
функциональной геометрии имеет огромную цену в проекте. Это обводы самолетов и
судов, профили крыльев, кузовные поверхности автомобилей, профили и рабочие
поверхности лопаток турбин.
Кроме
изделий этих отраслей есть большое количество технических изделий в промышленности,
строительстве, в промышленном дизайне, которые также требуют геометрии высокого
качества. Это направляющие кривые и поверхности почвообрабатывающих агрегатов,
трассы дорог, профили плоских кулачков, рабочие поверхности лопаток и
импеллеров насосов, внешняя геометрия изделий промдизайна.
Известны
т.н. топовые CAD-системы, которые предлагают
методы моделирования т.н. кривых и поверхностей класса высокого качества
(класса А).
На
предприятии “ООО С3Д Лабс” разрабатывается геометрическое ядро C3D, нативное для
КОМПАС 3D. К настоящему времени разработан раздел C3D FairCurveModeler для моделирования кривых линий и поверхностей
высокого качества, кривых и поверхностей класса F (functional). Как
показывает тестирование методов, качество кривых и поверхностей класса F на порядок превышает качество кривых и поверхностей
класса A.
Уважаемые
российские конструкторы / дизайнеры, воспользуйтесь уникальным шансом. Пора
выходить из-под высокомерной опеки Запада. Применяйте отечественное ПО.
Применение раздела C3D FairCurveModeler
и его приложений быстрый и дешевый путь улучшения проектных характеристик
технических изделий! Пора делать отрыв, а не плестись в хвосте технологической
гонки с Западом.
Инновационный
раздел геометрического ядра C3D FairCurveModeler [1 2021 САПР и Графика] сформирован путем адаптации ПМK FairCurveModeler [2 2018 ПМК] под стандарты
оформления программ C3D. Раздел C3D FairCurveModeler также получил значительное развитие в период с 2019 года по 2024 год. Раздел
был дополнен инновационными методами сглаживания кривых на зашумленных точках,
построения кривых с монотонной кривизной, моделирования кривых нерегулярной
формы.
В
свою очередь, ПМK
FairCurveModeler было расширено новыми методами C3D FairCurveModeler. ПМK FairCurveModeler и C3D FairCurveModeler к настоящему времени синхронизированы по
функциональности. Но отличаются по
представлению в программах структур данных и способам обращения к стандартным
библиотекам векторной алгебры.
Отметим,
что, благодаря более простому представлению геометрических данных, близкому к
базовым представлениям C/C++, производительность работы ПМК FairCurveModeler выше.
Приложения
ПМК FairCurveModeler [2 2018 ПМК] также прошли адаптацию на основе расширенного
функционала ПМК. Предлагаем Вашему вниманию самое простое приложение
(прикладную библиотеку FairCurveModeler_2D.rtw для КОМПАС
ГРАФИК). Функционал приложения расширен ровно настолько, чтобы показать
разработчикам САПР / приложений САПР и пользователям FairCurveModeler_2D.rtw
базовые возможности ПМК / C3D FairCurveModeler.
Данное
приложение может служить расширенным дополнением (или заменителем?) команды
‘Метасплайн’ КОМПАС версий 2021, 2022, 2023 [3 КОМПАС 3D], разработанной на
основе C3D FairCurveModeler. Команда ‘Метасплайн’ КОМПАС не раскрывает всего
потенциала C3D FairCurveModeler,
особенно, в плане геометрического редактирования кривой.
Приложение
FairCurveModeler_3D.rtw реализует полный инструментарий FairCurveModeler для моделирования и редактирования кривых.
В
следующей статье мы опишем приложение FairCurveModeler_3D.rtw для моделирования
функциональных пространственных кривых и поверхностей высокого качества в
КОМПАС 3D.
1. Геометрические
определители
В
качестве исходных геометрических данных для построения кривых используются
геометрические определители (ГО) 3-х видов:
-
опорная ломаная;
-
касательная ломаная;
-
ГО Эрмита. ГО Эрмита представляет собой опорную ломаную, в вершинах которой
фиксированы векторы касательных и векторы кривизны.
В
системе FairCurveModeler_2D.rtw ГО Эрмита реализован в виде ломаной, которая
последовательно обходит вершины опорной ломаной, концы векторов касательных,
концы векторов кривизны.
**
Ограничения представления ГО Эрмита в приложении.
При
больших размерах геометрического объекта величина вектора кривизны может стать
меньше точности представления объекта в CAD-системе. И система просто округлит значения кривизны
до нуля. Поэтому до перехода на ГО Эрмита отмасштабируйте геометрический объект
(ломаную или NURBzS кривую) так, чтобы объект
поместился в стандартный формат чертежа, например, А0. Масштаб запишите в
основную надпись чертежа.
Это
касается и очень маленьких объектов. Но не из-за возможного исчезновения
кривизны, а из-за близости соседних точек. Масштаб для увеличения объекта
должен быть таким, чтобы объект был хорошо виден на чертеже произвольного
стандартного формата.
2. Качественные кривые
Изогеометричность
и высокое качество кривых по критериям плавности – это “альфа и омега” системы FairCurveModeler.
Изогеометричность
означает, что форма моделируемой кривой должна быть подобна форме исходного ГО.
Дополнительные параметры, задающие форму кривой, вида касательных в вершинах
опорной ломаной не должны противоречить форме ломаной.
Высокое
качество кривых по критериям плавности означает:
-
высокий порядок гладкости,
-
минимальное число вершин (экстремумов кривизны),
-
малое значение потенциальной энергии кривой,
-
ограниченная скорость изменения кривизны.
Именно
эти качества кривых обеспечивают высокие
проектные характеристики технических изделий с функциональными кривыми и
поверхностями.
Метод
построения кривых высокого качества основан на алгоритмическом способе
изогеометрического построения виртуальной кривой (V-кривой) высокого качества. После генерации точек и
параметров V-кривой, на сгенерированных
точках и параметрах изогеометрически строятся рациональная сплайновая кривая
Безье (NURBzS кривая) или B-сплайновая
кривая (NURBS кривая).
Построение
кривой может быть глобальным или локальным.
Построение V-кривой является глобальным.
Одновременно учитываются все параметры ГО. Также глобальным является
аппроксимация V-кривой посредством B-сплайновой кривой. Аппроксимация V-кривой является локальной. Учитываются параметры
ограниченного участка ГО.
Базовой
аналитической кривой V-кривой
является кривая 2-го порядка (как полином у полиномиальных сплайнов). Благодаря
этому V-кривая геометрически точно моделирует К2П (как
полиномиальные сплайны геометрически точно полиномы). Свойство точного
моделирования окружностей, эллипсов в технике является необходимостью [4 Levien ].
Удачное
название V-кривой введено в КОМПАС 3D. Термин Метасплайн подчеркивает более общий подход к
построению глобальных кривых.
3. Установка и вызов и
Приложения:
1)
скачайте FairCurveModeler2D.zip;
2)
разархивируйте архив FairCurveModeler2D.zip;
3)
ознакомьтесь с лицензионным соглашением 'License.pdf';
4)
перенесите на диск C:\ папку FairCurveModeler_TEMP;
5)
загрузите КОМПАС и с помощью менеджера библиотек подключите прикладную
библиотеку FairCurveModeler2D_x64.rtw или FairCurveModeler2D_Win32.rtw.
6)
в документе КОМПАС ГРАФИК вызовите из вкладки ‘Приложения’ приложение
FairCurveModeler_2D (рис. 1).
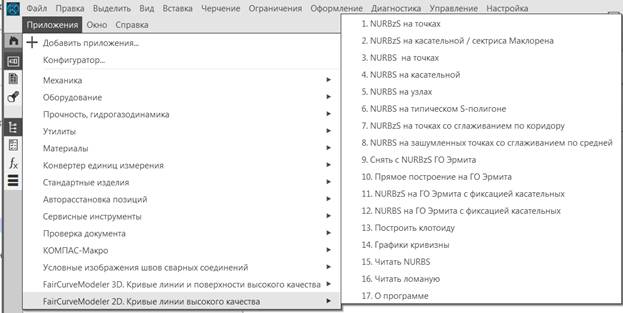
Рис. 3.1. Вызов приложения FairCurveModeler_2D.
4. Команды Приложения
1. NURBzS на точках
Команда
изогеометрически строит V-кривую на
опорной ломаной или на опорной ломаной ГО Эрмита и аппроксимирует V-кривую посредством NURBzS кривой.
По
умолчанию кривая строится с однократным уплотнением.
2. NURBzS на касательной
Команда
изогеометрически строит V-кривую на
касательной ломаной или на касательных ГО Эрмита и аппроксимирует V-кривую посредством NURBzS кривой.
По
умолчанию кривая строится с однократным уплотнением.
3. NURBS на точках
Команда
изогеометрически строит V-кривую на
опорной ломаной или на опорной ломаной ГО Эрмита и аппроксимирует V-кривую посредством B-сплайновой кривой 8-ой степени (9-го порядка).
По
умолчанию кривая строится с однократным уплотнением.
4. NURBS на касательной
Команда
изогеометрически строит V-кривую на касательной ломаной или на касательных ГО
Эрмита и аппроксимирует V-кривую посредством B-сплайновой кривой 8-ой степени (9-го порядка).
По
умолчанию кривая строится с однократным уплотнением.
5. NURBS на узлах
Команда
строит B-сплайновую кривую 7-ой степени (8-го порядка) на
ломаной так, что узловые точки сплайна совпадают с вершинами исходной ломаной.
6. NURBS на
типическом S-полигоне
Команда формирует типический S-полигон в открытом формате и определяет NURBS кривую с монотонной кривизной.
7. NURBzS на точках со сглаживанием по
коридору
Сглаживает
/ улучшает кривую на ломаной / ГО Эрмита в заданном коридоре отклонений кривой
от исходного положения.
8. NURBS на зашумленных точках со
сглаживанием по средней
Строит
кривую на ломаной / ГО Эрмита и ломаной зашумленных точек, деформируя исходную
опорную ломаную таким образом, что, построенная на деформированной опорной
ломаной, кривая представляет собой некоторую среднюю линию, сумма отклонений от
которой зашумленных точек равна нулю.
9. Снять с NURBzS ГО Эрмита
Команда
формирует на исходной кривой ГО в виде опорной ломаной, касательной ломаной или
в виде ГО Эрмита.
10. Прямое построение на ГО Эрмита
Команда
строит NURBzS кривую непосредственно на параметрах ГО Эрмита без
построения V-кривой.
11. NURBzS на ГО Эрмита с фиксацией
касательных
Уникальная
опция – фиксация касательных на глобальном сплайне. Можно задавать
фиксированные касательные в точках опорной ломаной ГО Эрмита. Предварительно
необходимо построить на NURBzS кривой ГО
Эрмита и скорректировать касательные векторы ГО Эрмита. Фиксированные вершины
должны перемежаться с вершинами без фиксации. В результирующей кривой точки,
смежные к точкам с фиксацией будут изменены.
Для
того, чтобы не менять позиции исходных точек, можно предварительно построить на
исходном ГО Эрмита NURBzS кривую с уплотнением и
перейти на ГО Эрмита уплотненной кривой.
12. NURBS на ГО Эрмита с фиксацией
касательных
Предварительно
необходимо на кривой выполнить команду “11. NURBzS на ГО Эрмита с фиксацией
касательных” и определить ГО Эрмита на скорректированной NURBzS кривой.
При этом точки фиксации на ГО Эрмита должны
совпадать с точками фиксации из предыдущей команды.
Ограничение.
Количество точек без фиксации между точками с фиксацией / концевыми точками / точками перегиба должно быть равно степени m NURBS
кривой, деленое на 2.
Для
того, чтобы удовлетворить данному ограничению, можно повторно определить ГО
Эрмита на скорректированной NURBzS кривой с
уплотнением и повторить определение ГО Эрмита на уплотненной NURBzS кривой.
Фиксацию
в концевых точках не задавать! Учитываются по умолчанию.
13. Построить клотоиду
Команда
строит клотоиду и аппроксимирует посредством NURBzS кривой с сохранением линейности изменения кривизны. В
качестве исходных данных задается длина начального участка клотоиды, радиус
кривизны в конечной точке и количество сегментов аппроксимирующей NURBzS кривой.
14. Графики кривизны
Команда
рисует графики кривизны и эволюты кривой.
15. Читать NURBS
Команда
читает из Геометрического Буфера (из папки C:\FairCurveModeler_TEMP\Temp) модель NURBS кривой (файл spl_name.spl).
16. Читать ломаную
Команда
читает из Геометрического Буфера (из папки C:\FairCurveModeler_TEMP\Temp) ломаную
(файл pnt_name.pnt).
11. О программе
Отображает
информацию о разработчиках.
5. Редактирование кривой
на дуальных ГО
Из
теории конических кривых известно свойство дуальности представления коники.
Одну и ту же конику можно определить, как на точках, так и на касательных. В FairCurveModeler дуальность ГО – это возможность редактирования одной
и той же кривой на двух дуальных видах ГО (на опорной ломаной и на
касательных). Это полезно при редактировании кривой. Пусть кривая построена на
опорной ломаной или касательной. Переходим к ГО Эрмита (команда “6. Снять с
NURBzS ГО Эрмита”). Далее редактируем ГО Эрмита. Изменяем координаты вершин и
при опциях "1. NURBzS на точках" / "3. NURBS на точках"
строим кривую на опорной ломаной ГО Эрмита. Изменяем направления касательных в
ГО Эрмита и при опциях "2. NURBzS на касательной" / "4. NURBS на
касательной" строим кривую на касательных ГО Эрмита. Фиксируем изменения
кривой в новом ГО Эрмита.
Дуальный метод редактирования кривых
инновационно расширяет инструментарий дизайнера / конструктора.
Пример
Пусть
была построена NURBzS по точкам (рис. 1)_.
Необходимо обеспечить точные габаритные размеры контура.
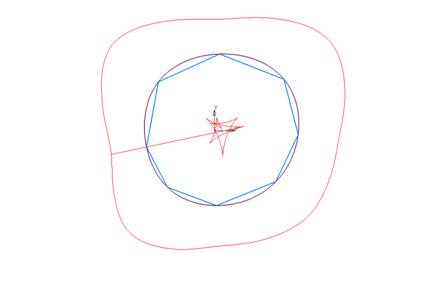
Рис.
5.1. Кривая на опорной ломаной. Графики кривизны и эволюты.
Необходимо
обеспечить габариты по крайним точкам опорной ломаной. Это должен глобальный
сплайн высокого порядка гладкости.
Переходим
на ГО Эрмита (рис. 2).
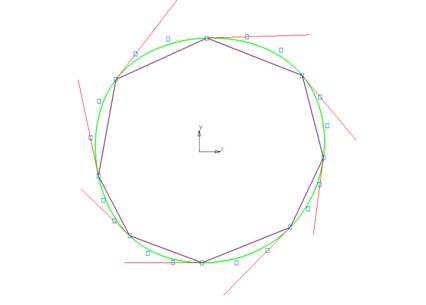
Рис.
5.2. ГО Эрмита.
ГO Эрмита позволяет строить V-кривую на опорной ломаной и на касательных. При этом
кривая не меняется. Именно в этом смысле ГО Эрмита – это дуальный
геометрический определитель. Отредактируем ГО Эрмита. Нам необходимо ограничить
габариты кривой по крайним точкам опорной ломаной. Отредактируем ГО Эрмита.
Выставим направления касательных в крайних точках по вертикали и горизонтали
(рис. 3).
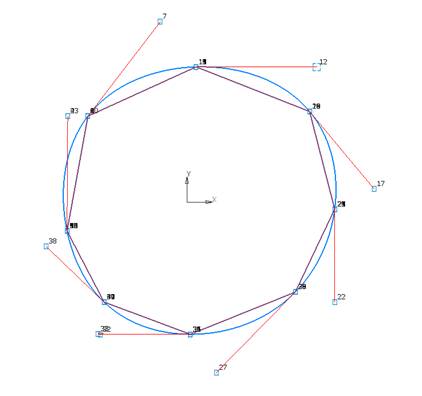
Рис.
5.3. Отредактированный ГО Эрмита.
Построим
глобальный сплайна (V-кривую) на касательных ГО Эрмита
(рис. 4).
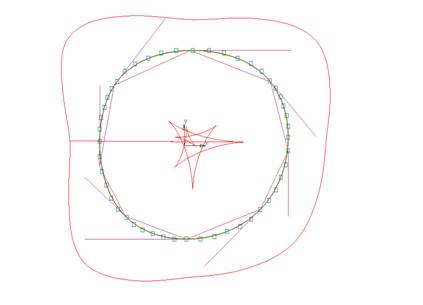
Рис.
5.4. Метасплайн на касательных.
Получили
плавную кривую, точно ограниченную по габаритам исходной опорной ломаной.
Именно такой способ редактирования должна обеспечивать команда ‘Метасплайн’ в
КОМПАС 3D.
Кривая
на касательных, но отошла от опорных точек (рис. 5).
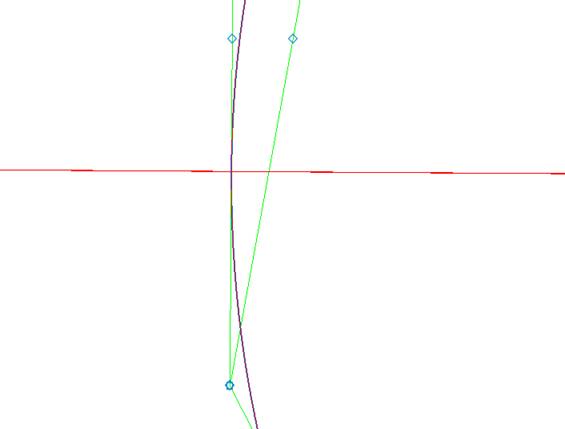
Рис.
5.5. Отход кривой от опорных точек.
Это
цена за качество кривой.
Получили
плавную кривую, точно ограниченную по габаритам исходной опорной ломаной.
6. Особенности
редактирования с фиксацией касательных
Стандартная процедура
Рассмотрим
процедуру фиксации на примере моделирования аэродинамического контура (рис. 1).

Рис.
6.1. Исходная ломаная.
Необходимо
построить кривую с фиксированными касательными в 0-ой точке, во 2-ой и 4-ой
точке.
Предварительно
строим NURBzS кривую
с параметрами по умолчанию, но без уплотнения (рис. 2).

Рис.
6.2. Предварительное построение NURBzS
кривой без уплотнения.
Формируем
ГО Эрмита (команда “9. Снять с NURBzS ГО Эрмита”)(рис. 3).

Рис.
6.3. ГО Эрмита на NURBzS кривой.
Редактируем
ГО Эрмита. Устанавливаем вертикальную касательную в 0-ой точке, горизонтальную касательную
во 2-ой точке (рис. 4).

Рис.
4. Отредактированный ГО Эрмита.
Удаляем NURBzS
кривую и определяем NURBzS кривую
с фиксацией касательных (команда "11. NURBzS на ГО Эрмита с фиксацией касательных"). Указываем номера
точек 0, 2, 4. Построенная NURBzS кривая
имеет заданные касательные (рис. 5).
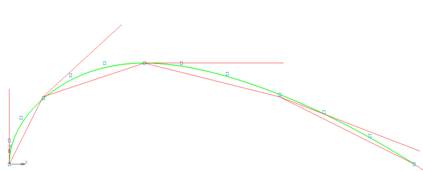
Рис. 6.5. NURBzS кривая
с заданными касательными.
Повторим
определение ГО Эрмита на отредактированной NURBzS кривой
(рис. 6).

Рис. 6.6. ГО Эрмита на отредактированной кривой.
Аппроксимация B-сплайновой кривой
Для
построения B-сплайновой кривой с фиксацией
касательных необходимо чтобы между точками с фиксацией были m/2 точек без фиксации. Для этого выполним следующие
процедуры.
Перестроим
NURBzS кривую
с уплотнением (рис. 9) и определим ГО Эрмита (рис. 8).

Рис. 6.8. NURBzS с уплотнением

Рис.
6.9. Уплотненный ГО Эрмита.
Теперь
между точками с фиксацией есть три точки. Можно строить B-сплайновую кривую степени 6 с фиксацией касательных в
точке с номером 4 (рис. 10).

Рис.6.10.
B-сплайновая кривая с
фиксированными касательными.
NURBzS и NURBS кривые
на чертеже совпадают.
Обратите
внимание на графики кривизны. Обеспечивается монотонность кривизны.
Такая
техника фиксации, которая начинается с построения NURBzS без уплотнения,
позволяет обеспечить такую же плавность кривизны, как на исходной кривой
(рис. 4).
Фиксация с сохранением позиций исходных
точек опорной ломаной
Можно
при редактировании оставить нетронутыми все исходные точки опорной ломаной. Для
этого нужно начинать процедуру с построения NURBzS кривой с
уплотнением (рис. 11).

Рис.
11. Построение NURBzS с уплотнением.
После
выполнения всех процедур, описанных в предыдущем примере, мы получим следующий
результат (рис. 12).

Рис.
6.12. NURBzS
с фиксированной касательной в точке 4
опорной ломаной.
Графики
кривизны стали несколько хуже, чем в примере (рис. 11). Нет монотонности
кривизны.
Настоятельно
рекомендуем использовать технику фиксации касательных без предварительного
уплотнения NURBzS кривой предварительного построения.
Особенности фиксации касательных в
точках замкнутой кривой
Предположим
у нас есть замкнутый контур из предыдущего примера (рис. 13)
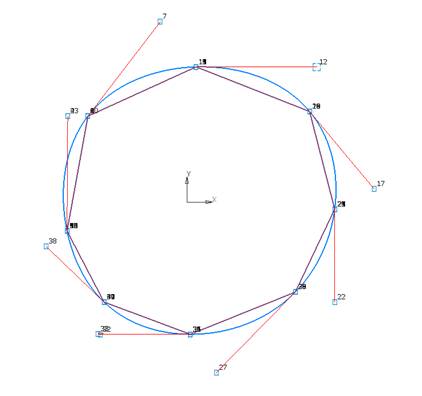
Рис.
6.13. Отредактированный ГО Эрмита.
И
так, мы отредактировали ГО Эрмита. В крайних точках опорной ломаной касательные
вертикальны или горизонтальны.
Выполним
команду “11. NURBzS на ГО Эрмита с фиксацией
касательных” построения кривой на опорной ломаной с фиксацией касательных.
Зафиксируем касательные в вершинах 0, 2, 4, 6 (рис. 14).
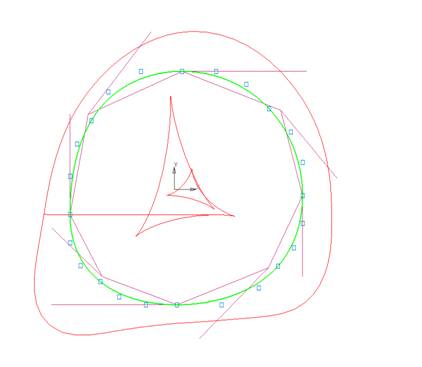
Рис.
6.14. Учет касательных.
7. Прямое построение
кривых на ГО Эрмита
ГО
Эрмита также позволяет строить кривые произвольной формы. При этой опции -
кривая строится непосредственно по параметрам ГО Эрмита без построения
V-кривой.
Гибкое редактирование. Иногда после построения требуется отредактировать
кривую с нарушением изогеометричности. Для этих целей вполне подходит метод
прямого редактирования NURBzS кривой на ГО Эрмита. Можно локально менять позиции
вершин, направления касательных, значения кривизны. Метод обеспечивает
неограниченную гибкость моделирования с контролем формы. Возможны произвольные
формы кривых.
Данный
метод в комбинации с методами построения V-кривой позволяет радикально расширить область
допустимых форм моделируемой кривой.
Можно
готовить ГО Эрмита независимо от построения V-кривой. Например, подготовим ГО Эрмита, взяв 4 точки
на окружности (рис. 1). Не соблюдая условия регулярности.
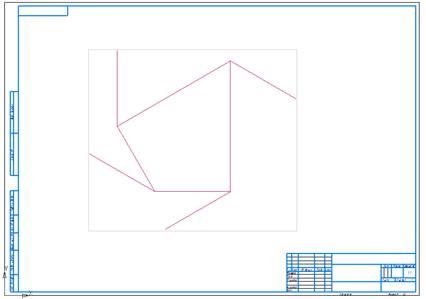
Рис. 7.1.
ГО Эрмита, снятая с окружности.
Методом
прямой локальной аппроксимации на ГО Эрмита построим NURBzS кривую (рис. 2).
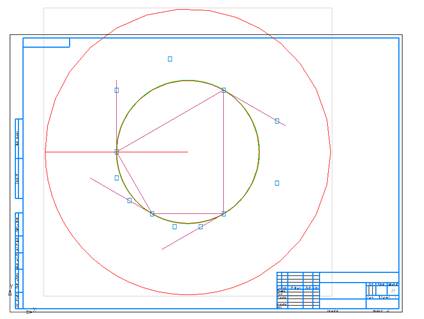
Рис.
7.2. Аппроксимация кривой на ГО Эрмита, снятой с окружности.
Отредактируем
ГО Эрмита. Изменим произвольно направление касательной в одной из точек. Повторим
построение (рис. 3).
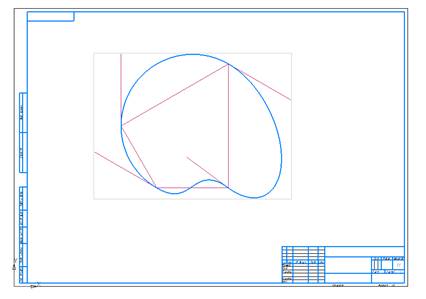
Рис. 7.3.
Кривая, отредактированная на ГО Эрмита.
Построим
глобальный сплайн на опорной с фиксацией касательных в крайних точках.
Доводка кривых
В
частности, метод может использоваться для доводки кривых, построенных с опцией
улучшения.
Например,
рассмотрим этап построения кривой (рис. 7) после редактирования ГО Эрмита с
установкой касательных по габаритам (рис. 4).

Рис.
7.4. Отредактированный ГО Эрмита.
Перестроим
кривую на ГО Эрмита прямым методом (команда “10. Прямое построение на ГО
Эрмита”) (рис. 5).
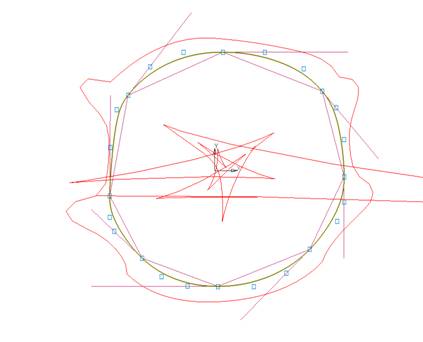
Рис.
7.5. Прямое редактирование ГО Эрмита.
Плавность
нарушилась. Но сохранился 2-ой порядок гладкости.
Фиксация аналитических кривых. Качественные
кривые не ограничиваются V-кривыми. Оптимальными
кривыми в проектах могут кривые из золотого фонда замечательных кривых.
Например, цепная линия, линия наискорейшего спуска, эластика.
8. Улучшение
традиционных сплайнов
Традиционный
подход построения сплайна заключается в том, что сплайн определяется по условию
совпадения узлов сплайна с точками исходной ломаной. В приложении команда “NURBS на узлах” строит
NURBS 7-степени. Точки принимаются за узлы сплайна (рис. 1).
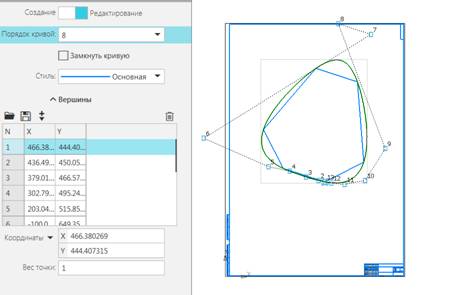
Рис. 8.1. Традиционная B-сплайновая кривая 7-ой степени (8-го порядка),
построенная по узлам.
Точки
ломаной сняты с окружности, но сплайн ни разу не похож на окружность.
В
системе FairCurveModeler построение B-сплайновой
кривой – это праздник.
Например,
построим B-кривую 8-ой степени на той же
ломаной с опцией гармонизации (рис. 2).
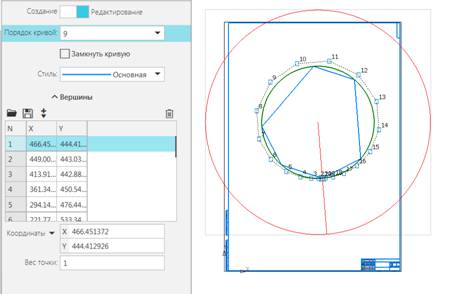
Рис.
8.2. B-сплайновая кривая 8-ой степени (9-го порядка).
Известны
способы улучшения качества построения сплайнов по узлам путем подбора
параметрической сетки с неравномерным шагом, например, пропорциональным длине
отрезка ломаной. Возможны другие ухищрения.
Например,
вот как проходит сплайн степени 7 через точки окружности в CAD-системе NX [5 NX ](рис. 3).
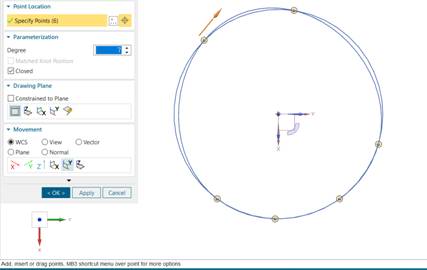
Рис.
8.3. Сплайн через точки окружности в NX.
Намного
лучше, чем в примере (рис. 1), но не идеально. Кривые класса A при
всех ухищрениях не удовлетворяют требованию геометрически точного моделирования
К2П [Левьен].
Есть
еще одна “подлянка” от применения параметрических сеток с неравномерным шагом.
Способ применения неравномерной параметрической сетки абсолютно неприемлем для B-сплайновой поверхности r (U, V), при построении которой используются единые
параметрические сетки по U и по V.
Однако,
не все так плохо для кривых класса A. На
регулярных ломаных, предварительно использовав опцию гармоничного распределения
вершин на V-кривой, вы можете построить
традиционный сплайн с таким высоким качеством, который не снился разработчикам
кривых класса А (рис. 4).
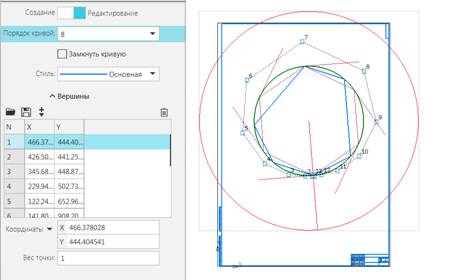
Рис.
8.4. B-сплайновая кривая 7-ой степени (8-го порядка), построенная по узлам с
опцией гармонизации.
Как
видим, на улице сплайнов по узлам теперь тоже праздник. И все это, благодаря V-кривой и опции гармонизации.
Разумеется, для окружности легко подобрать гармоничную
ломаную. Это просто многоугольник с равными сторонами. Построим ломаную на
эллипсе с неравномерным распределением вершин по контуру кривой (рис. 5).
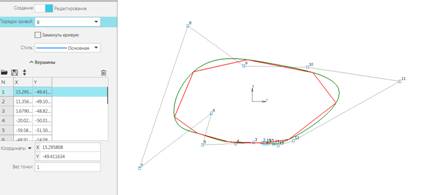
Рис.
5. NURBS 7-ой степени по узлам на исходной ломаной.
Построим
NURBzS кривую
с опцией гармонизации и перейдем к ГО вида ломаной.
На
гармонизированной ломаной построим B-сплайновую
кривую по узлам (рис. 6 )
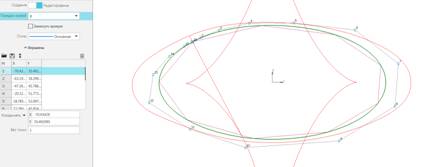
Рис.
8.6. NURBS 7-ой степени по узлам на гармонизированной ломаной.
NURBS визуально совпадает с эллипсом. Фантастическая
эффективность опции гармонизации! И это обыкновенная B-сплайновая кривая на равномерной сетке с единичными
весами.
Разработчики
кривых класса A должны обратить на это внимание. Считаем, для них
система C3D FairCurveModeler является эффективным средством улучшения качества
кривых класса A. По крайней мере, на ломаных,
снятых с конических кривых.
Внимание!
Для качественного построения сплайна по узлам с опцией гармонизации требуется
регулярность формы ломаной.
9. Эстетические кривые
Спирали
Для
определения “настоящих” по красоте эстетических кривых были введены т.н. Log-эстетические кривые [6 Log-эстетика, 7 Log-эстетика
+]. Если отбросить псевдонаучную “шелуху” вокруг эстетики крыла бабочки и линии
лезвия катаны, то log-эстетические кривые — это
спирали с линейной кривизной на логарифмической шкале. Также в класс log-эстетических кривых неожиданно добавляются окружность
и клотоида.
Отметим,
что мы, авторы данной работы, считаем самыми красивыми те кривые, которые
оптимальным образом определяют функциональную геометрию изделий. В общем
случае, красивые кривые – это плавные кривые, критерии плавности которых
описаны в п. “Качественные кривые” [8 Муфтеев Эстетика кривых].
Однако
в некоторых случаях требуется строгая монотонность кривизны или, даже, точный
вид графика кривизны, например, при проектировании трассы дороги [9
Проектирование трассы с клотоидой]. Клотоидные вставки с линейным графиком
кривизны обеспечивают точный контроль центробежных сил, действующих на
транспортное средство на виражах.
Радикальное
решение формирования спиралей произвольных форм был предложен в работе [10
Зиатдинов Р.А. Суперспираль]. Алгоритм построения т.н. суперспирали позволяет
сформировать любую спиральную кривую, в том числе, все известные спирали и все log-эстетические кривые. Формула суперспирали Зиатдинова
реализована в системе Mathematica [11
Mathematica].
Вид
суперспирали Зиатдинова зависит от тройки параметров (a, b, c) (рис. 1)

Рис.
9.1. Задаются параметры формы суперспирали в виде тройки (a, b, c).
При
данных параметрах формируется логарифмическая спираль (рис. 10).
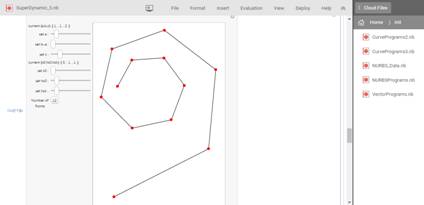
Рис.
9.10. Формируется ГО
Затем
ГО Эрмита переносится в приложение и прямым методом строится NURBzS кривая
(рис. 11).

Рис.
9.11. Логарифмическая спираль в чертеже.
Отобразим
графики кривизны и эволюты построенной спирали (рис. 12).
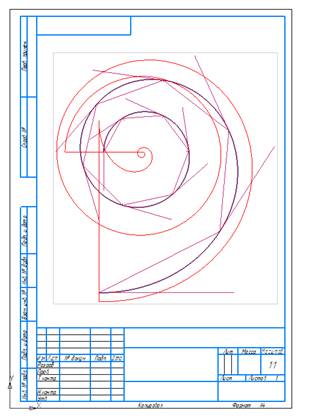
Рис.
9.12. Графики кривизны и эволюты суперспирали.
Аппроксимирующая
NURBzS кривая
сохраняет качество аналитической кривой.
Клотоида и сектриса Маклорена
Две
уникальные кривые с монотонной кривизной введены в систему.
1)
Клотоида строится по команде “Clothoid”.
Строится начальный участок клотоиды. Задается длина участка и значение радиуса
кривизны на конце участка (рис. 13)
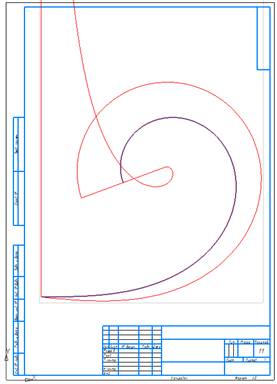
Рис.
9.13. Клотоида с параметрами (длина участка = 500, конечный радиус= 50,
количество сегментов NURBzS кривой =
12);
Метод построения кривой в соприкасающемся треугольнике
с монотонной кривизной разработан авторами [12 Муфтеев Сектриса] на основе
результатов исследований Зиатдиновым Р.А. [13 Зиатдинов Сектриса] формулы
сектрисы Маклорена. При углах <90 градусов при основании соприкасающегося
треугольника кривая строго монотонна.
2)
Сектриса Маклорена строится командой “2. NURBzS на касательной / сектриса Маклорена” при задании
двухзвенной касательной ломаной (рис. 14).

Рис.
9.14. Кривая с монотонной кривизной в соприкасающемся треугольнике. Показаны
графики кривизны и эволюты.
Типические кривые
Для
формирования кривых с монотонной кривизной проф. Farin’ым был предложен алгоритм генерации вершин B-полигона [14 Farin Typical curve].
В нашей работе [15 Муфтеев typical Curve] мы показали ошибочность использования
B-полигона, но подтвердили правильность подхода для S-полигона B-сплайновой
кривой.
В
приложении реализован алгоритм генерации вершин S-полигона в открытом формате (float).
Команда
построения “6. NURBS на типическом S-полигоне”. Исходная ломаная – двухзвенник
(рис. 15).
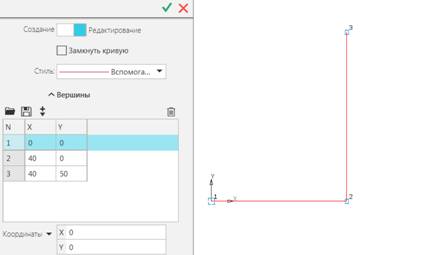
Рис.
9.15. Исходный 2-звенник.
Формируется
типический S-полигон (рис. 16).
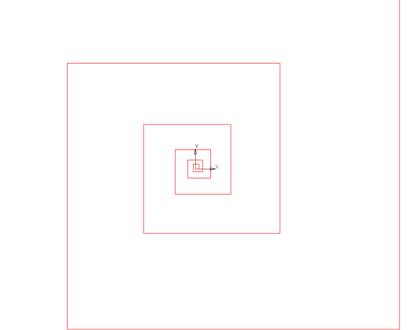
Рис.
10.16. Формируется типический S-полигон в
открытом формате (float).
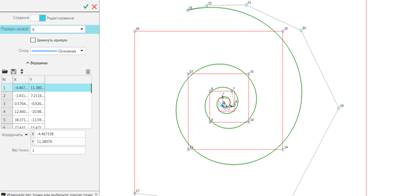
Рис.
9.17. На S-полигоне открытого формата формируется
NURBS кривая.
Аппроксимирующая
кривая сохраняет качество аналитической кривой (рис. 18).
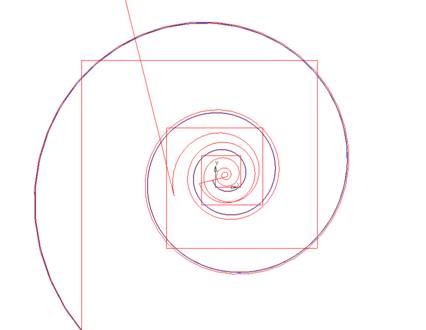
Рис.
9.18. NURBS-кривая 8-ой степени с монотонной кривизной. Графики кривизны и эволюты.
10. Улучшение /
сглаживание
1) Повышение качества плавности /
эстетичности
Можно
по-разному реализовать желание “сделайте мне красиво”. Уникальная опция
сглаживания позволяет реально делать плавные кривые еще более эстетичными.
В работе [16 Муфтеев
& Зинаншина 2022 Сглаживание] показано применение
метода сглаживания для эстетизациии кривых. Положим,
дизайнер нарисовал кривую, которую хочет использовать для моделирования объекта дизайна. Даже без
художественного образования понятно, что кривая «некрасивая». Однако после
сглаживания с коридором 10 мы получаем кривую, достойную кисти Рафаэля, а при
коридоре сглаживания 20 - это уже кривая Дали. Таким образом, даже неопытный
дизайнер может создать шедевр, используя метод сглаживания (рис. 1).

Рис. 1. Тест из работы [Муфтеев & Зинаншина
2022 Сглаживание].
2) Повышение устойчивости и улучшение качества при
фиксации касательных
Техника
улучшения
1)
Строим NURBzS с
улучшением без уплотнения на опорной ломаной;
2)
Формируем ГО Эрмита;
3)
Редактируем касательные;
4)
Строим NURBzS прямым
способом на ГО Эрмита;
5)
Уплотняем столько раз, сколько нужно для того, чтобы количество опорных точек
было > 5 между точками фиксации и ломаные через раз не имели острых углов;
6
Формируем ГО Эрмита;
7)
Строим NURBzS кривую
со сглаживанием по коридору с фиксацией касательных.
[8)
Формируем ГО Эрмита;
9) Строим NURBzS кривую с
фиксацией касательных.]
Построим
на замкнутой ломаной NURBzS кривую с
улучшением (рис. 2).

Рис. 10.2. Построение с улучшением без фиксации
касательных.
Определим
на кривой ГО Эрмита (рис. 3).

Рис.
10.3. ГО Эрмита на кривой.
Отредактируем
ГО Эрмита. Изменим касательные в крайних точках на вертикальные и
горизонтальные (рис. 4).
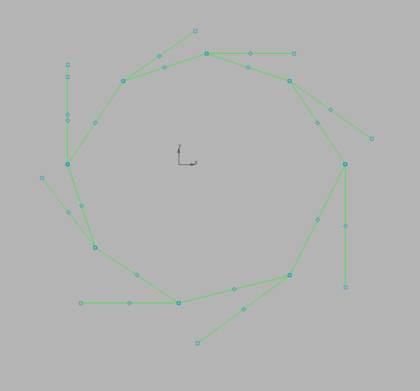
10.4.
Отредактированный ГО Эрмита.
Прямое
построение NURBzS кривой на отредактированном ГО Эрмита (рис. 5).
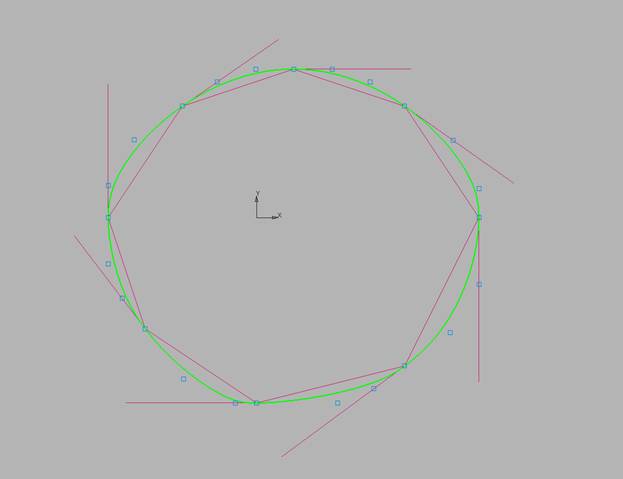
Рис.
10.5. Прямое построение.
Уплотним
NURBzS прямого
построения (рис. 6).
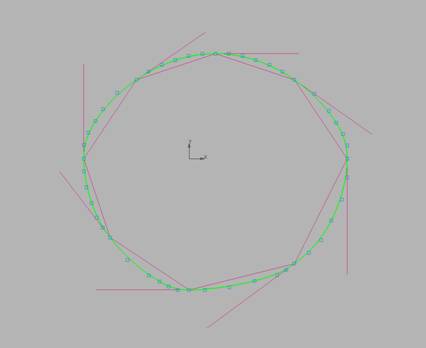
Рис.
10.6. Уплотненная NURBzS кривая.
Перейдем
к ГО Эрмита (рис. 7).
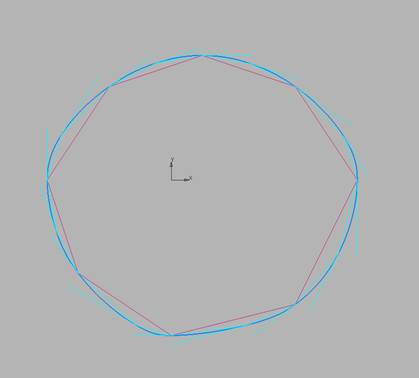
Рис. 10.7) ГО
Эрмита на уплотненной NURBzS
кривой прямого построения.
Удалим
кривую. Сгладим кривую. Установим параметры (итераций 30, коридор 10)(рис. 8).
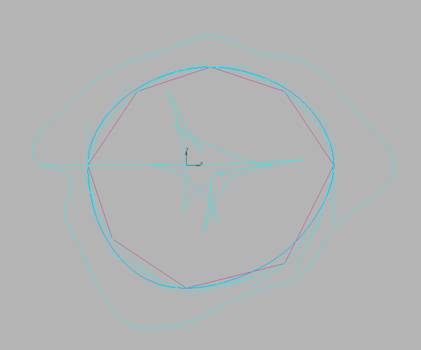
Рис.
10.8. Сглаженная NURBzS кривая.
Перейдем
к ГО Эрмита на сглаженной кривой (рис. 9).
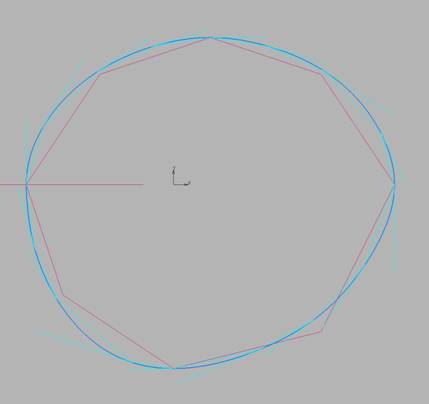
Рис.
10.9. ГО Эрмита сглаженной кривой.
Построим
кривые с фиксацией во всех точках. Теперь можно просто зафиксировать
касательные 0, 4, 8, 12 (рис. 10.10).
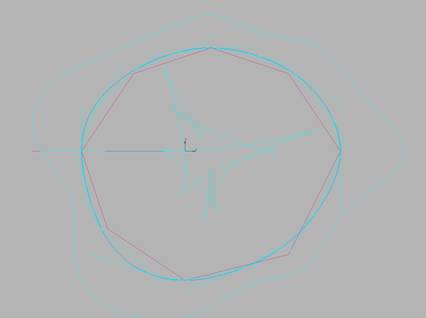
Рис.
10.10. NURBzS
кривая с фиксированными в точках 0, 4, 8,
12.
Опять
ГО Эрмита (рис. 11).

Рис.
10.11. Переход на ГО Эрмита.
Строим
NURBS с фиксацией 0, 4, 8, 12 (рис. 12).
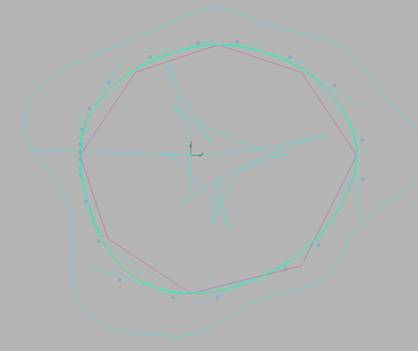
Рис. 10.12.
B-сплайновая кривая степени 6 с фиксированными
касательными крайних габаритных точках.
11. Правила построения
плавных кривых
Исходные
данные можно классифицировать по степени определенности структуры кривой:
- ломаная зашумленных точек;
-
ломаная нерегулярной формы;
-
регулярная ломаная;
- ломаная гармоничной формы.
Ломаная зашумленных точек
Данные
могут быть получены в результате измерения физических объектов на сканерах. Шум
возникает из-за погрешности измерения.
Другой
источник зашумленных данных – таблицы точек из архивов чертежей советской
эпохи. Шум – из-за погрешности округления.
Сплайн
строится на зашумленных данных командой “8. NURBS на зашумленных точках со
сглаживанием по средней”.
Нерегулярные ломаные
В
функционале C3D FairCurveModeler проработана устойчивость построения кривой на
ломаной произвольной формы (с острыми углами, пилообразной формы). Работает
алгоритм регуляризации ломаной с особенностями при сохранении изогеометричности
и условии ненарушения параметрами формы кривой.
Например,
пилообразная ломаная (рис. 1).
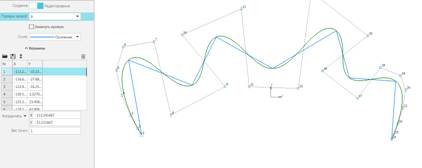
Рис.
11.1. B-кривая на пилообразной ломаной.
Однако,
при резких нерегулярностях нельзя ожидать высокого качества плавности кривой.
Например,
вершины ломаной принадлежат окружности, но один угол при вершине < 90
градусов. Это вызвало работу алгоритма регуляризации без применения V-кривой (рис.
2).
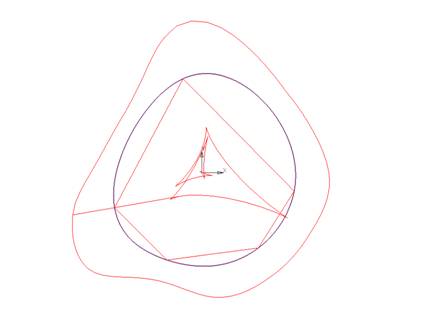
Рис.
11.2. Кривая на нерегулярной ломаной
Чтобы
исправить ситуацию, добавим точку на ломаной таким, образом, чтобы угол при
вершине превышал 90 (рис. 33).
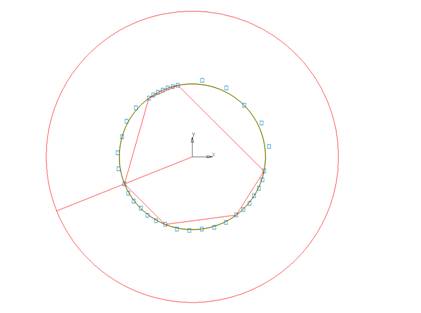
Рис.
11.3. Кривая на регулярной ломаной.
Внимание!
Только при соблюдении регулярности формы на 100 процентов обеспечивается
высокое качество кривых.
Регулярные ломаные
Для
построения высококачественных кривых по критериям плавности необходимо
придерживаться определенных правил.
Из
дифференциальной геометрии известно, что регулярная кривая – это гладкая
кривая. Гладкая кривая в каждой своей точке имеет единственную касательную.
Регулярную
кривую можно аппроксимировать направленной ломаной без совпадающих вершин и с
углами между звеньями-векторами меньше 90 градусов (или больше 90 градусов при вершинах
ломаной). Такую ломаную назовем регулярной ломаной. В определенном смысле,
регулярная ломаная будет подобна регулярной кривой. Верно и обратное, на
регулярной ломаной можно построить регулярную кривую, подобную ломаной. Кривая
должна проходить через точки, не выходить из областей, ограниченных прямыми
смежных звеньев, и не иметь перегибов на локально выпуклых участках ломаной.
По
форме регулярной ломаной можно вполне определенно судить о будущей форме
моделируемой кривой, что является необходимым фактором прогнозируемого
результата моделирования.
Гармоничная ломаная
Гармоничная
ломаная – регулярная ломаная, графики дифференциальных характеристик (вида
разделенных разностей) которой подобны графикам дифференциальных характеристик
(вида производных) моделируемой кривой.
С
точки зрения необходимости метрологической определенности геометрического
объекта на всех этапах проектирования и производства после построения
функциональной кривой дизайнер / конструктор должен сформировать комплексную
информационную модель кривой, содержащую NURBS модель и регулярную /
гармоничную ломаную, на которой построена кривая.
Это
необходимо для адекватного преобразования модели для CAM-систем и контроля
модели на этапах изготовления.
Именно
эти метрологические требования и обеспечивает система FairCurveModeler.
В
системе есть уникальная опция формирования ГО гармоничной формы. Это опция
гармонизирует форму исходной ломаной и улучшает качество кривой. Особенно эта
опция эффективна при аппроксимации V-кривой посредством B-сплайновой кривой.
Другие правила подготовки ГО:
1)
можно на опорной ломаной точно задавать точку перегиба. Точка перегиба должна
геометрически точно лежать на отрезке, который делит ломаную на данном участке
на ломаные разные формы (условно, на “выпуклую” и “вогнутую”).
2)
не рекомендуется задавать звенья ломаной с резким изменением длин и углов между
звеньями;
3)
прямолинейные участки задаются точками, точно лежащими на прямой;
4)
дополнительные параметры, которые задаются на ГО не должны противоречить форме
основной ломаной.
Другие ограничения:
1) при задании опорной ломаной с
прямолинейными участками и аппроксимации B-сплайновой кривой при обеспечении изогеометричности
точность аппроксимации будет меньше заданной. В этом случает
рекомендуется выполнить редактирование по методу, описанному в руководстве C3D FairCurveModeler [17 C3D FairCurveModeler].
2)
Алгоритм фиксации касательных построен на корректировке касательной в заданной
точке путем смещения смежных точек. При резком несоответствии направления
касательной форме исходной кривой при смещении смежных точек возможно нарушение
формы ломаной или вырождение результирующей кривой. В этом случае выводится
сообщение об ошибке.
Для
устранения ошибочной ситуации необходимо придерживаться двух стратегий:
1)
Предварительно
отредактировать исходную ломаную так, чтобы построенная кривая имела в заданных
точках касательные близкие к искомым.
2)
Придерживаться
техники, описанной в п. ‘10. Улучшение / сглаживание. 2) Повышение устойчивости и улучшение качества при фиксации
касательных’. При
построении кривой с фиксированными касательными необходимо последовательно
выполнить процедуры: построить NURBzS кривую без фиксации, определить на кривой ГО Эрмита,
отредактировать ГО Эрмита, построить прямым способом на ГО Эрмита NURBzS кривую,
уплотнить NURBzS,
перестроить на уплотненном NURBzS ГО Эрмита, построить на ГО Эрмита NURBS кривую со
сглаживанием по коридору и с фиксацией.
Правила
естественны и вытекают органично из теории кривых дифференциальной геометрии, требований
изогеометричности и согласуются с требованиями метрологической определенности
геометрических моделей в процессе проектирования и производства.
Технология построения кривых высокого
качества
Рекомендуем
следующую последовательность процедур построения:
1)
Переходим от зашумленных точек к регулярной кривой и формируем ГО Эрмита.
2)
Строим на регулярной ломаной кривую первого приближения и формируем ГО Эрмита с
регулярной ломаной;
3)
Редактируем ГО Эрмита (редактируем на дуальном ГО изменением конфигурации
опорной ломаной и направлений касательных, дополняем параметрами вида
фиксированных касательных, улучшаем сглаживанием по коридору отклонений,
гармонизируем опорную ломаную) для достижения заданной формы и качества кривой.
4)
Формируем и утверждаем документально окончательную комплексную модель кривой в
виде NURBS модели
и ГО Эрмита с регулярной или гармоничной опорной
ломаной. Размещаем на чертеже изображение функциональной кривой с указанием
масштаба. Н чертеже формируем таблицы с параметрами NURBS кривой
и с параметрами ГО Эрмита.
12. Сравнение с кривыми
класса A
Другой
веский довод в пользу предложенных правил построения кривых это то, что на
ломаных, подготовленных в рамках этих правил и ограничений, методы построения
кривых в FairCurveModeler показывают лучшие результаты по сравнению с известными
методами топовых систем, например, NX [5 NX].
Наше
почтение системе NX. Авторитетная топ система.
В
работе [18 класс F vs класс
A] проводится подробный сравнительный анализ кривых
класса A систем NX, Alias Design и кривых класса F системы C3D FairCurveModeler.
Анализ
показывает неоспоримое преимущество методов раздела C3D FairCurveModeler.
Покажем
это на простейших конфигурациях ломаных (рис.
1).

Рис.
12.1. Построение в NX сплайна
на ломаной для построения “профиля крыла”.
NX не
обеспечивает изогеометричности формы ломаной и
моделируемой кривой.
Рассмотрим
замкнутую конфигурацию (рис. 2).
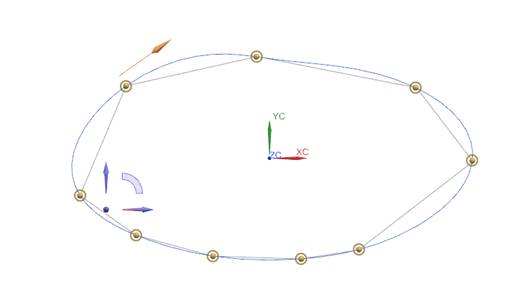
Рис.
12.2. Построение на замкнутой ломаной.
NX не
обеспечивает изогеометричности на простейшей
замкнутой ломаной.
Более
того, даже на гармонизированной ломаной NX не
обеспечивает изогеометричности (рис. 3).
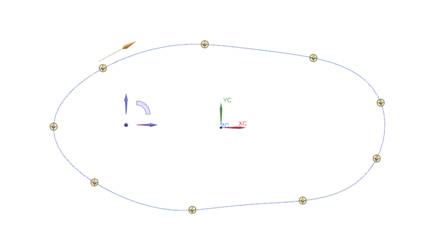
Рис.
12.3. Сплайн степени 7 на гармонизированной ломаной в NX.
В
то же время, в системе C3D FairCurveModeler обеспечивается изогеометрическое построение
сплайна по узлам и на равномерной параметрической сетке идеального качества
(рис. 8.6).
Глобальные
сплайны минимизируют некий глобальный функционал. Обычно, не вполне правомерно,
полиномиальные сплайны увязывают с минимизацией потенциальной энергии. Но
именно Метасплайн обеспечивают малое значение реальной потенциальной энергии
кривой. Более того, в нашей работе [19 V-curve
vs Физ. сплайн] показывается, что Метасплайн, построенный
на точках деформации физического сплайна, обладает меньшей потенциальной
энергией. Фантастика? Можете перепроверить. Все данные в статье [19 V-curve
vs Физ. сплайн].
Сравним
потенциальные энергии кривых, построенных в системе C3D и в NX. Замкнутые
кривые строятся на одной и той же ломаной, изогеометричны с исходными данными и
одинаковой степени (рис. 4).
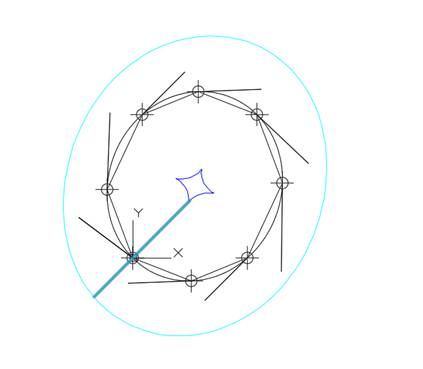
Рис. 12.4. Построение в FairCurveModeler
"Potential Energy =
" 0.0942002
"Min Curvature
= " 0.0126468
"Max Curvature
= " 0.0173732
Определим
потенциальную энергию кривой NX (рис. 5).
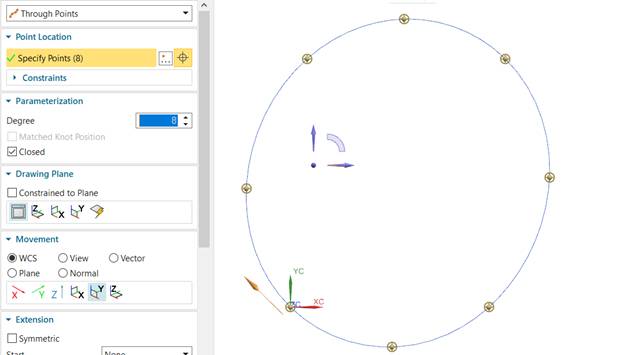
Рис.
12.5. Кривая в NX.
Измерим
в системе FairCurveModeler 3D (рис. 6).
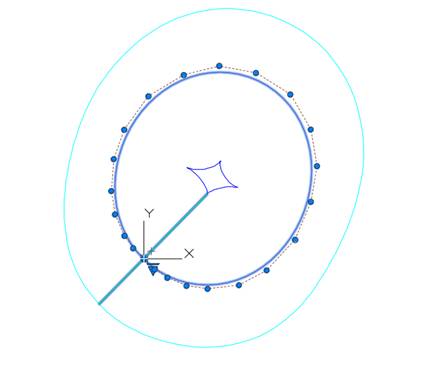
Рис. 12.6. Графики кривизны кривой из NX.
Измеренные параметры:
"Potential Energy =
" 0.094241
"Min Curvature = "
0.0121374
"Max Curvature
= " 0.0170172
(/
0.0942002 0.094241) = 0.999567
Качество
кривых на данной ломаной практически одинаково.
Ухудшим
конфигурацию ломаной (рис. 7).
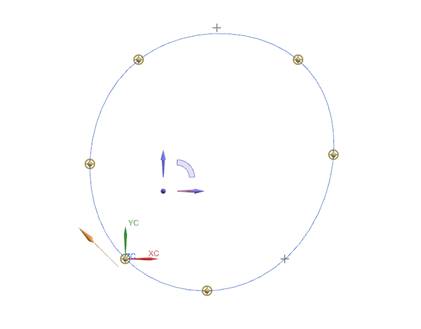
Рис.
12.7. Кривая на ухудшенной конфигурации
ломаной.
"Potential Energy =
" 0.0953648
"Min Curvature = "
0.0112446
"Max Curvature = "
0.0198427
Перестроим
кривую на этих же данных в FairCurveModeler
(рис. )
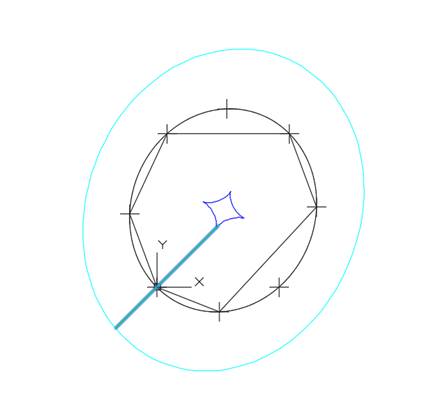
Рис. Кривая в FairCurveModeler.
Параметры:
"Potential Energy =
" 0.0942321
"Min Curvature = "
0.0126196
"Max Curvature = "
0.0174512
(/
0.0942321 0.0953648) = 0.988122
Чем
хуже конфигурация ломаной, тем сравнительно лучше
кривая в FairCurveModeler.
Выводы
В
статье рассмотрено приложение КОМПАС ГРАФИК FairCurveModeler_2D.rtw для моделирования кривых линий высокого качества
(класса F), разработанное на основе функционала C3D FairCurveModeler.
Кратко описаны команды приложения.
Предложен способ редактирования кривой на дуальных
видах геометрического определителя в качестве улучшения команды “Метасплайн” в
КОМПАС 3D.
Предложен способ улучшения метода построения B-сплайновых кривых на узловых точках с помощью опции
гармонизации ломаной на V-кривой.
Показаны возможности построения и редактирования
кривых с обеспечением фиксации касательных в точках исходной ломаной.
Предложено использовать метод прямого моделирования и
редактирования на ГО Эрмита для 1) моделирования и гибкого редактирования
кривых произвольной формы и 2) высококачественной аппроксимации аналитических
кривых.
Проведен сравнительный анализ методов построения
кривых класса A в NX и кривых класса F в C3D FairCurveModeler. Показывается преимущество методов C3D FairCurveModeler перед методами моделирования кривых класса A в NX Spline Studio.
Приложение может использоваться и в документах 3D для пространственного моделирования процедурных
поверхностей при подготовке эскизов кривых высокого качества.
Уважаемые
российские конструкторы / дизайнеры, воспользуйтесь уникальным шансом. Пора
выходить из-под высокомерной опеки Запада. Применяйте отечественное ПО.
Применение раздела C3D FairCurveModeler
и его приложений быстрый и дешевый путь улучшения проектных характеристик
технических изделий! Пора делать отрыв, а не плестись в хвосте технологической
гонки с Западом.
Библиография
[1
2021 САПР и Графика] Муфтеев В., Максименко А. Функциональные
кривые высокого качества - инновация в геометрическом моделировании от C3D Labs // САПР и графика. 2021. № 5 (295). С. 62-72.
[2
2018 ПМК] Программа FAIRCURVEMODELER моделирования
кривых и поверхностей класса "f" и разработка на ее основе прикладных
САПР / Муфтеев В. Г., Зиатдинов Р.Л., Зелев А. П.,
Набиев Р. И., Марданов А. Р., Ахметшин
Р. И., Талыпов М.А. // Электротехнические и
информационные комплексы и системы. 2018. Т. 14. № 2. С. 53-63.
[3
КОМПАС 3D] КОМПАС 3D. https://kompas.ru/?ysclid=m4dtlolfaw662613691
[4 Levien] Levien, R. L. From Spiral to Spline: Optimal Techniques in
Interactive Curve Design. PhD.thesis, University of California, Berkeley, 2009.
[5 NX]
https://www.syssoft.ru/softpower/siemens-nx-sapr-dlya-nepreryvnogo-razvitiya/?ysclid=m4dtx3egql791137968
[6 Log-эстетика] Y., Endo S., Maekawa T. Surface design based on
direct curvature editing // Computer-Aided Design. 2014. V. 55. P. 1—12.
[7 Log-эстетика +] Harada T. Study of quantitative analysis of the
characteristics of a curve // Forma. 1997. N. 12. V. 1. P. 55—63.
[8 Муфтеев Эстетика кривых] Muftejev V., Ziatdinov R.,
Nabiyev R. Multi-criteria assessment of shape quality
in cad systems of the future // GraphiCon 2020. В сборнике: CEUR Workshop Proceedings. "Proceedings
of the 30th International Conference on Computer Graphics and Machine
Vision". 30 Cep. 2020.
[9
Проектирование трассы с клотоидой] Проектирование
автомобильных дорог в IndorCAD / И.В. Кривых, Д.А.
Петренко, В.Н. Бойков и др. - Томск: Изд-во Том. ун-та, 2015. - 406 с. -.
[10 Зиатдинов Р.А. Суперспираль] Ziatdinov R. Family of superspirals
with completely monotonic curvature given in terms of Gauss hypergeometric
function // Computer Aided Geometric Design. 2012. № 29. V. 7. P. 510-518.
[11
Mathematica] https://www.wolfram.com/mathematica/
[12
Муфтеев Сектриса] РАЗРАБОТКА И СОВЕРШЕНСТВОВАНИЕ
МЕТОДОВ И ПРИЛОЖЕНИЙ C3D©FAIRCURVEMODELER / Муфтеев В.Г., Зиганшина Ф.Т.,
Гумеров В.И. / Труды Международной конференции по компьютерной графике и зрению
"Графикон". 2023. № 33. С. 840-847.
[13 Зиатдинов Сектриса] Ziatdinov Rushan, Kim Tae-wan, Nabiyev Rifkat I. Two-point G1 Hermite interpolation in biangular
coordinates // Journal of computational and Applied Mathematics 287. 2015.
P.1-11.
[14 Farin Typical curve] Farin G. Class A Bézier curves // Computer Aided Geometric Design.
2006. № 23. V. 7. P. 573—581.
[15 Муфтеев typical Curve] Rushan
Ziatdinov, Valerijan Muftejev, Rifkat
Nabiyev, Albert Mardanov, Rustam Akhmetshin. Techniques for
modeling high-quality B-spline curves by S-polygons in a float format /
Geometric Modeling. Computer Graphics in Education GraphiCon
2018.
[16 Муфтеев & Зинаншина 2022 Сглаживание] Эволюционный алгоритм сглаживания кривой на массиве зашумленных точек. http://spliner.ru/Publications/paper_092.pdf
[17
C3D FairCurveModeler] C3D FairCurevModeler. Тестирование методов моделирования кривых. http://spliner.ru/Publications/22_testirovanie_metodov_modelirovanija_krivykh.pdf
[18
класс F vs класс
A] Кривые класса F vs кривых класса A. http://spliner.ru/appKOMPAS3D/FCM_vs_.pdf
[19
V-curve
vs Физ. сплайн] Эволюционный алгоритм сглаживания кривой
на массиве
зашумленных точек. http://spliner.ru/Publications/2024_mufteev-c3d_fsm_vs_elastic.pdf