Программа может использоваться при проектировании технических объектов с криволинейными динамическими поверхностями, активно взаимодействующими со средой. К таким техническим объектам относятся объекты, проектируемые в авиастроении, судостроении, автомобилестроении, в сельхозмашиностроении. К геометрическим характеристикам динамических поверхностей предъявляются высокие требования по критериям плавности. Методы моделирования кривых линий и поверхностей обеспечивают высокий порядок гладкости и заданный закон изменения кривизны по направлению потока среды. Программа FairCurveModeler предназначена для моделирования функциональных кривых и поверхностей класса F(Functional).

Простое улучшение геометрии изделия с помощью методов FairCurevModeler существенно повышает проектные характеристики изделия.

Сравнительное тестирование показывает абсолютное преимущество методов моделирования кривых и поверхностей класса F приложений FairCurveModeler перед методами моделирования кривых и поверхностей класса A в NX , AliasDesign и др. (см. сравнение моделирования кривых и поверхностей).

В 2025 году в течение всего года действует акция разработчиков. Разработчик предоставляет Вам продукт с бесплатной лицензией. Скачать архив с Программой можно по ссылке (прикладная библиотека КОМПАС 3D).

Для работы с программой FairSurfaceModeler должен быть открыт документ 3D.

Геометрические объекты программы FairCurveModeler 3D имеют атрибуты. Каждый тип геометрического объекта имеет свой тип атрибута. Атрибутов может быть несколько. Сложные геометрические объекты представляют собой макрообъекты. Все типы атрибутов заданы в библиотеке атрибутов SModel.lat.

Геометрические определители

В качестве исходных геометрических данных для построения кривых используются геометрические определители (ГО) 3-х видов:

- опорная ломаная;

- касательная ломаная;

- ГО Эрмита. ГО Эрмита представляет собой опорную ломаную, в вершинах которой фиксированы векторы касательных и векторы кривизны.

В системе FairCurveModeler_2D.rtw ГО Эрмита реализован в виде ломаной, которая последовательно обходит вершины опорной ломаной, концы векторов касательных, концы векторов кривизны.

** Ограничения представления ГО Эрмита в приложении.

При больших размерах геометрического объекта величина вектора кривизны может стать меньше точности представления объекта в CAD-системе. И система просто округлит значения кривизны до нуля. Поэтому до перехода на ГО Эрмита отмасштабируйте геометрический объект (ломаную или NURBzS кривую) так, чтобы объект поместился в стандартный формат чертежа, например, А0. Масштаб запишите в основную надпись чертежа.

Это касается и очень маленьких объектов. Но не из-за возможного исчезновения кривизны, а из-за близости соседних точек. Масштаб для увеличения объекта должен быть таким, чтобы объект был хорошо виден на чертеже произвольного стандартного формата.

Качественные кривые

Изогеометричность и высокое качество кривых по критериям плавности – это “альфа и омега” системы FairCurveModeler.

Изогеометричность означает, что форма моделируемой кривой должна быть подобна форме исходного ГО. Дополнительные параметры, задающие форму кривой, вида касательных в вершинах опорной ломаной не должны противоречить форме ломаной.

Высокое качество кривых по критериям плавности означает:

- высокий порядок гладкости,

- минимальное число вершин (экстремумов кривизны),

- малое значение потенциальной энергии кривой,

- ограниченная скорость изменения кривизны.

Именно эти качества кривых обеспечивают высокие проектные характеристики технических изделий с функциональными кривыми и поверхностями.

Метод построения кривых высокого качества основан на алгоритмическом способе изогеометрического построения виртуальной кривой (V-кривой) высокого качества. После генерации точек и параметров V-кривой, на сгенерированных точках и параметрах изогеометрически строятся рациональная сплайновая кривая Безье (NURBzS кривая) или B-сплайновая кривая (NURBS кривая).

Построение кривой может быть глобальным или локальным. Построение V-кривой является глобальным. Одновременно учитываются все параметры ГО. Также глобальным является аппроксимация V-кривой посредством B-сплайновой кривой. Аппроксимация V-кривой является локальной. Учитываются параметры ограниченного участка ГО.

Базовой аналитической кривой V-кривой является кривая 2-го порядка (как полином у полиномиальных сплайнов). Благодаря этому V-кривая геометрически точно моделирует К2П (как полиномиальные сплайны геометрически точно полиномы). Свойство точного моделирования окружностей, эллипсов в технике является необходимостью [Levien ].

Удачное название V-кривой введено в КОМПАС 3D. Термин Метасплайн подчеркивает более общий подход к построению глобальных кривых.

На каркасе ломаных или на каркасе кривых можно определять B-поверхности.

Установка и вызов и Приложения:

1) скачайте FairCurveModeler3D;

2) разархивируйте архив FairCurveModeler3D;

3) ознакомьтесь с лицензионным соглашением 'Лицензия.pdf';

4) перенесите на диск C:\ папку FairCurveModeler_TEMP;

5) загрузите КОМПАС и с помощью менеджера библиотек подключите прикладную библиотеку FairCurveModeler3D_x64.rtw или FairCurveModeler3D_Win32.rtw.

6) в документе КОМПАС 3D вызовите из вкладки ‘Приложения’ приложение FairCurveModeler_3D (рис. 1).

Рис. 1. Вызов приложения.

Меню команд

V-кривые, аппроксимированные ГО Эрмита

1. Построить ГО Эрмита на ломаной

2. Построить ГО Эрмита на касательной ломаной

Команды строят V-кривую (виртуальную кривую) на опорной ломаной, на касательной ломаной или на ГО Эрмита.

V-кривая на выпуклых участках кривой является огибающей непрерывного семейства К2П и принадлежит классу кривых 5-ого порядка гладкости. V-кривая аналитического выражения не имеет.

Для представления v-кривой на чертеже в системе КОМПАС 3D используется шаблон V-кривой в виде ГО Эрмита или шаблон V-кривой в виде B-кривой (B-сплайновой кривой) 8-ой степени (9-го порядка).

ГО Эрмита аппроксимирует V-кривую с точностью до значений кривизны и закона изменения кривизны V-кривой.

При построении кривой на касательной ломаной V-кривая соприкасается со звеньями исходной полилинии. V-кривая точно моделирует прямолинейные участки кривой. Для моделирования прямолинейных участков три или более точек ломаной должны лежать на одной прямой.

При построении V-кривой на ломаной можно задавать граничные параметры: касательные векторы и кривизну.

Для задания граничных параметров вида касательного вектора и кривизны формируется макроэлемент. Макроэлемент состоит из трех геометрических объектов. Первый, граничный объект, – пространственная ломаная из одного или двух звеньев. Второй, основной объект, – пространственная ломаная. Третий, граничный объект, - пространственная ломаная из одного или двух звеньев.

Граничный элемент вида ломаной из одного звена определяет касательный вектор.
Граничный элемент вида ломаной из двух звеньев определяет касательный вектор и радиус кривизны. При коллинеарности звеньев определяется нулевая кривизна.
При построении кривой на касательной ломаной граничные объекты игнорируются.
Для анализа качества кривых линий выводятся графики кривизны и центров кривизны.
Можно установить пространственные преобразования (см. п. Преобразования).

Можно изменить параметры построения: степень уплотнения. Можно изменить опции улучшения (убрать улучшение, ввести признак гармонизации). Можно исходную опорную ломаную рассматривать как расширенную. Концевые звенья расширенной ломаной представляют векторы касательных.

Исходная ломаная может представлять собой ГО Эрмита второго порядка фиксации. Ломаная ГО Эрмита обходит опорные точки вершины касательных векторов и вершины векторов кривизны.

V-кривые, аппроксимированные B-кривыми

1. Построить B-кривую на ломаной

2. Построить B-кривую на касательной ломаной

Команды строят V-кривую на опорной ломаной или на касательной ломаной.
V-кривая (виртуальная кривая) на выпуклых участках кривой является огибающей непрерывного семейства К2П и принадлежит классу кривых 5-ого порядка гладкости. V-кривая аналитического выражения не имеет.

V-кривая аппроксимируется B-кривой (B-cплайновой кривой на равномерной сетке с единичными весами).

Выделите ломаную в дереве построения. Вызовите соответствующую команду построения из Меню. Можно использовать параметры построения по умолчанию (в этом случае фиксируются следующие параметры: степень B-кривой - 8, однократное уплотнение).

Можно изменить параметры построения: степень B-кривой, степень уплотнения. Можно изменить опции улучшения (убрать улучшение, ввести признак гармонизации). Можно исходную опорную ломаную рассматривать как расширенную. Концевые звенья расширенной ломаной представляют векторы касательных.

Построенные B-кривые можно редактировать с помощью управляющих полигонов.
Всегда есть возможность редактирования отдельной B-кривой из каркаса B-кривых на исходной ломаной или на ГО Эрмита. Для перехода к редактированию на ГО Эрмита выполняется построение “Снять ГО с репараметризацией кривой”. На ГО Эрмита можно положения опорных точек, менять направления касательных и значения кривизны.

Эстетические кривые

1. Клотоида

Команда строит кривую с монотонной линейной кривизной, начиная с нулевого значения. Задаются концевое значение радиуса кривизны, длина участка и количество сегментов, аппроксимирующего ГО Эрмита. Можно перейти к аппроксимации B-кривой.

2. Сектриса Маклорена

Команда строит кривую с монотонной кривизной в соприкасающемся треугольнике. В дереве построения выделяется ломаная из двух звеньев. Ограничение: углы при основании соприкасающегося треугольника должны быть <= 90 градусов. Аппроксимирующий ГО Эрмита имеет 10 сегментов. Можно перейти к аппроксимации B-кривой.

3. Типическая ломаная

Команда формирует типический S-полигон в открытом формате и определяет NURBS кривую с монотонной кривизной.

Операции над кривыми

1. Снять ГО с репараметризацией кривой

Команда по заданной опции опорную ломаную / касательную ломаную / ГО Эрмита второго порядка фиксации с заданным числом узловых точек. Используется NURBS кривая произвольного формата.

2. Копировать кривую

Команда копирует объект с помощью пространственного преобразования.
Предварительно установите пространственные преобразования (см. п. Преобразования).
Выделите в дереве построения объект копирования. Выполните команду “Копировать кривую”.

3. Переместить кривую

Команда перемещает отдельную кривую с помощью пространственного преобразования. Применяется для редактирования отдельной кривой каркаса кривых.
Предварительно установите пространственные преобразования (см. п. Преобразования).
Выделите в дереве построения объект. Выполните команду “Переместить кривую”.

4. Замкнуть/разомкнуть В-кривую

Команда преобразует формат замкнутых кривых. Закрытый (Clamped) формат преобразуется в открытый (float) и наоборот.

Операции над каркасами

1. Собрать кривые в каркас

Объединяет отдельные кривые в один каркас. Формирует макроэлемент “Каркас ломаных”.

Выделите в дереве построения по порядку расположения на поверхности все кривые. Выполните команду “Собрать кривые в каркас”.

2. Выделить каркас направляющих

Транспонирует сеть точек, определенную каркасом ломаных / карасом S-полигонов кривых.

Выделите в дереве построения макроэлемент “Каркас ломаных” / "Каркас NURBS". Выполните команду “Выделить каркас направляющих”. Сформируется макроэлемент “Каркас направляющих”.

3. Замкнуть/разомкнуть ломаные каркаса

Замыкает незамкнутые ломаные / размыкает замкнутые ломаные.

4. Снять каркасы ломаных с грани

Укажите на объекте грань. Выполните команду “Снять каркасы ломаных с грани”.
Задайте количество точек для образующей ломаной и направляющей ломаной.
Сформируются два макроэлемента – каркас образующих ломаных с граничными параметрами и каркас направляющих ломаных с граничными параметрами.
Ломаная каркаса формируется вместе с граничными параметрами вида касательного вектора (касательные векторы выделяются красным и зеленым цветом).
Можно установить пространственные преобразования (см. п. Преобразования).

Поверхности

1. Определить поверхность

Команда формирует определитель / модель поверхности.

Исходные геометрические определители

1) Каркас образующих NURBS кривых

2) Каркас образующих NURBS кривых
и / или

3) Каркас направляющих NURBS кривых.

Результат

Результат – определитель NURBS поверхности.

Формирование каркаса образующих ломаных

Создайте набор ломаных, согласованных по количеству сегментов и признаку замкнутости.

Пространственная ломаная создается командой КОМПАС 3D “Операция” – “Пространственные кривые” – “Ломаная”.

Выделите в дереве построения ломаные по порядку их расположения на моделируемой поверхности. Объедините их в каркас ломаных командой Программы “Собрать кривые в каркас”.

Формирование каркаса образующих и направляющих NURBS кривых

Выделите в дереве построения “Каркас ломаных”. Восстановите на каркасе ломаных каркас NURBS кривых командой Программы “Построить NURBS кривую на ломаной” или командой “Построить NURBS кривую на касательной ломаной”.

Выделите в дереве построения “Каркас NURBS”. Выделите из каркаса NURBS кривых каркас направляющих ломаных, проходящих по вершинам NURBS кривых командой Программы “Выделить каркас направляющих”.

Выделите в дереве построения “Каркас направляющих”. Восстановите на каркасе направляющих ломаных каркас направляющих NURBS кривых командой Программы “Построить NURBS кривую на ломаной”.

Примечание. Каркас направляющих ломаных выделяйте только на каркасе NURBS кривых. Не используйте для формирования поверхности каркас направляющих ломаных, выделенных на каркасе ломаных.

Формирование каркаса направляющих NURBS кривых

Произвольный каркас NURBS кривых принимается за каркас направляющих NURBS кривых NURBS поверхности.

Редактирование NURBS поверхности выполняется с помощью управляющих точек направляющих NURBS кривых.

Раскройте ветвь макроэлемента “NURBS поверхность”. Выделите редактируемый Сплайн. В контекстном меню нажмите строку “Редактировать”. Отредактируйте сплайн.
Порядок непрерывности поверхности при редактировании сохраняется. Можно контролировать качество направляющих кривых командой Программы “Графики кривизны”. При редактировании нельзя изменять количество точек и признак замкнутости кривых.

Всегда есть возможность редактирования направляющих NURBS кривых на опорных точках направляющей NURBS кривой.

Для перехода к редактированию на опорных точках с граничными параметрами выделите редактируемую NURBS кривую в каркасе направляющих и выполните команды "Репараметризация" (формируется NURBzS кривая с заданным числом узловых точек) > “Снять ГО Эрмита с NURBzS кривой”. После редактирования ГО Эрмита восстановите редактируемую сплайновую кривую. При этом в дереве построения ломаную ГО Эрмита и редактируемую NURBS кривую. Сплайновая кривая изменится восстановлением на ломаной опорных точек.

Примечание

Опорные точки направляющей NURBS кривой не принадлежат моделируемой поверхности.

2. Построить поверхность

Исходный объект – геометрический определитель поверхности или сеть точек, заданная каркасом ломаных.

Результат - поверхность в формате “Imported Surface”.

Примитив “Imported Surface” определяется на сети интерполированных точек поверхности.

Поверхность “Imported Surface” является uv-плазовой поверхностью, определенной на сети пространственных кубических сплайнов. При невысоких требованиях к качеству поверхности и точности задания граничных параметров и прямолинейных участков можно строить поверхности непосредственно на каркасах ломаных, минуя этапы построения каркасов сплайновых кривых высокого качества для формирования определителя поверхности.

Предварительно установите параметры интерполяции, эквидистанты, аффинных преобразований и параметры деформации поверхности (морфинга) (см. п. Преобразования).

Выделите в дереве построения определитель поверхности. Если установлены параметры деформации поверхности (морфинга), то дополнительно выделите две кривые – функции деформации образующих и направляющих линий поверхности.
Выполните команду “Построить поверхность”.

Результирующий объект можно оставить в чертеже в виде каркаса интерполированных ломаных или сразу в виде поверхности в формате “Imported Surface”.

Каркас интерполированных ломаных с поверхности можно использовать для снятия точек с поверхности или грани. А также для построения пространственной кривой с привязкой к точкам ломаных каркаса.

В дальнейшем каркас интерполированных точек можно перевести в поверхность в формате ”Imported Surface” командой “Построить поверхность”.

Тестирование кривых

1. Графики кривизны

Укажите (выделите) в дереве построения сплайновую кривую. Выполните команду “Графики кривизны”.

Программа отображает графики кривизны сплайновую кривую (красного цвета), кривую центров кривизны (зеленого цвета), график кривизны (синего цвета).
Графики кривизны формируются как пространственные ломаные и их можно оставить в 3D документе.

Интерполированную ломаную сплайновой кривой можно использовать для перепараметризации сплайновой кривой с другой ломаной опорных точек.
График центров кривизны можно использовать для формирования граничных параметров.

Импорт объектов их геометрического буфера

1. Импорт ломаной

2. Импорт сплайновой кривой

3. Импорт поверхности

В специальном буфере программы сохраняются результирующие объекты. Буфер может использоваться для следующих целей:

1. Для совместной работы с Приложением FairCurveModeler (ZWCAD / BricsCAD / nanoCAD).

2. Для копирования результирующих объектов в данной программе с пространственными преобразованиями в пространстве детали.
Выполните команду “Импорт ломаной” / “Импорт сплайновой кривой” / “Импорт поверхности” в зависимости от того, что было создано в приложениях FairCurveModeler.

Преобразования

1. Установить преобразования

2. Отключить преобразования

Перед выполнением команды из меню программы FairCurveModeler 3D задаются необходимые для выполнения данной команды параметры в соответствующих атрибутах объекта с данными. Объект с данными это геометрический объект с атрибутами или пустой макрообъект с атрибутами. После подготовки данных в атрибутах выделяется объект с данными и выполняется команда “Установить преобразования”.

После этого необходимо в дереве построения выделить геометрические объекты, которые нужны для выполнения данной команды из меню, и выполнить команду из меню.
После выполнения команды выполняется команда “Отключить преобразования”.
Это общая схема выполнения команды из меню.

Команда: 1. Установить преобразования

Включает флаги преобразований и формирует параметры преобразований.
Выделите в дереве построений объект с атрибутами преобразований. Выполните команду “Установить преобразования”.

В зависимости от того, какие атрибуты прикреплены к объекту, команда включает флаг соответствующих преобразований и формирует параметры преобразований по параметрам атрибутов

Команда: 2. Отключить преобразования

Отключает флаги всех преобразований.
Устанавливает значения параметров по умолчанию.

1. Преобразовать в пространстве. Параметры масштабирования, вращения, переноса

Над кривыми линиями и поверхностями можно выполнять пространственные преобразования масштабирования, вращения и переноса. На поверхности можно строить эквидистантную поверхность. Поверхность можно деформировать по двум заданным кривым функциям деформации образующих и направляющих линий поверхности.

Все параметры преобразований задаются в атрибутах из библиотеки атрибутов SModel.lat. Атрибут “Преобразовать” используется для задания пространственных преобразований. Атрибут “Эквидистанта” – для установки параметров интерполяции и радиуса эквидистанты. Атрибут “Рельеф” – для установки параметров деформации (морфинга) поверхности. Задаются зона деформации на области определения [u,v] поверхности r(u,v), вектор направления деформации, масштабный коэффициент деформации.

Пароль для редактирования атрибутов “111”.

Атрибуты пространственных преобразований и определения эквидистанты можно прикрепить к произвольному объекту.

Рекомендуется создавать пустые макроэлементы в качестве контейнеров для атрибутов преобразований. Например, для параметров пространственных преобразований можно создать макроэлемент с именем “Перенос”, “Вращение” или “Масштаб”. Для параметров интерполяции и эквидистанты - макроэлемент “Эквидистанта 20 шаг U 0.2 шаг V 0.1”.

Образцы атрибутов “Эквидистанта” со значениями параметров по умолчанию, “Преобразования” c параметрами тождественного преобразования, “Рельеф” с зоной деформации, совпадающей с областью определения поверхности, единичным масштабным коэффициентом и направлением вектора деформации по направлению нормали к поверхности, создаются при выполнении команды “Определить поверхность” и прикрепляется к определителю поверхности.

Параметры преобразований

Параметры пространственные преобразования кривых и поверхностей

Параметры аффинных преобразований устанавливаются в атрибуте “Преобразования”.

Образец тождественного преобразования:

base 0. 0. 0. – базовая точка для последующих преобразований
scale 1. 1. 1. – масштабирование по осям X,Y,Z;
radian 0. 0. 0.– вращение в радианах вокруг осей X,Y,Z;
grade 0. 0. 0. – вращение в градусах вокруг осей X,Y,Z;
move 0. 0. 0. – перенос по осям X,Y,Z.

Можно вводить неограниченное число строк, менять базовую точку.

2. Определить эквидистантную поверхность. Параметры интерполяции поверхности и радиус эквидистанты

Параметры интерполяции поверхности и радиус эквидистанты
Установите параметры интерполяции поверхности и радиус эквидистанты в атрибуте “Эквидистанта”.

Задайте параметры интерполяции сплайновой поверхности при преобразованиях - количество отрезков, аппроксимирующих сегмент образующей сплайновой кривой и количество отрезков, аппроксимирующих сегмент направляющей сплайновой кривой,
Задайте радиус эквидистанты.

О программе

(C)FairCurveModeler. Ver (2005 - 2016)

Программа моделирования кривых и поверхностей высокого качества. Разработчики: Муфтеев В.Г., Мударисов С.Г., Марданов А.Р. Фархутдинов И.М. г.Уфа, БГАУ, кафедра НГ и графики, кафедра с/х машиностроения.
e-mail:muftejev@mail.ru

(C)FairCurveModeler. Ver (2017 - 2024)

Программа моделирования кривых и поверхностей высокого качества. Разработчики: Муфтеев В.Г., Зиганшина Ф.Т., Ефимова Г.М., Набиев Р., Ахметшин Р., Фаттахов М.М. г.Уфа, УГАТУ, кафедра ОКМиМ; УГНТУ, кафедра комплексного инжиниринга и компьютерной графики, кафедра технологии дорожного строительства.
e-mail:muftejev@mail.ru

(C)FairCurveModeler. Ver (2024 - 2025)

Программа моделирования кривых и поверхностей высокого качества. Разработчики: Муфтеев В.Г., Зиганшина Ф.Т., Ефимова Г.М., Набиев Р., Ахметшин Р., Гумеров В.И., г.Уфа, УГАТУ, кафедра ОКМиМ; УГНТУ, кафедра комплексного инжиниринга и компьютерной графики, кафедра технологии дорожного строительства.
e-mail:muftejev@mail.ru

Сравнительное тестирование методов построения B-поверхности

Построение B-поверхности степеней (8 * 8) с помощью прикладной библиотеки 'FairCurveModeler 3D.rtw’ КОМПАС 3D

Пусть дан набор ломаных, точки которой сняты с примитива _Torus (см. Приложение). Откройте файл torus_pllns.m3d (рис. 1).

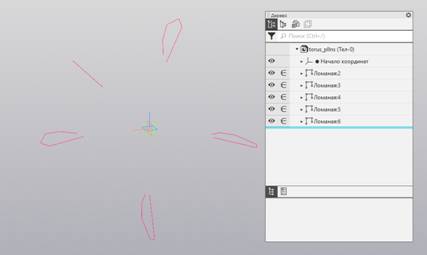
Рис. 1. Исходный набор ломаных.

Построим B-поверхность степеней 8,8 командами 'FairCurveModeler 3D.rtw’ КОМПАС на этих ломаных.

Выделим последовательно все ломаные по порядку и объединим в каркас ломаных командой (рис. 2):

Операции над каркасами

1. Собрать кривые в каркас

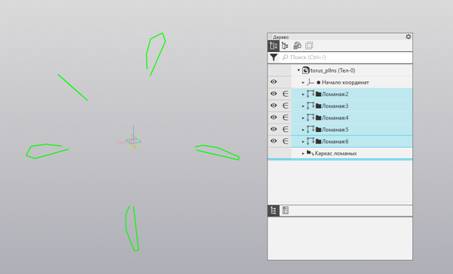
Рис. 2. Ломаные объединены в каркас ломаных.

Замкнем все ломаные каркаса командой

Операции над каркасами

3. Замкнуть / разомкнуть ломаные каркаса

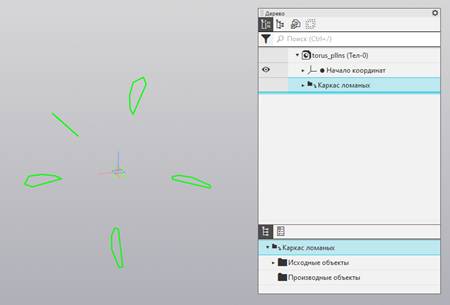
Рис. 3. Ломаные каркаса замкнуты

Построим на замкнутых ломаных образующие B-кривые степени 8 командой

NURBS кривые

1. Построить NURBS кривую на ломаной

Параметры дадим по умолчанию (рис. 4).

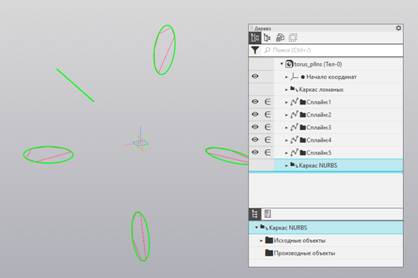
Рис. 4. Каркас образующих B-кривых степени 8.

Выделим направляющие ломаные каркаса S-полигонов образующих B-кривых командой (рис. 5)

Операции над каркасами

2. Выделить каркас направляющих

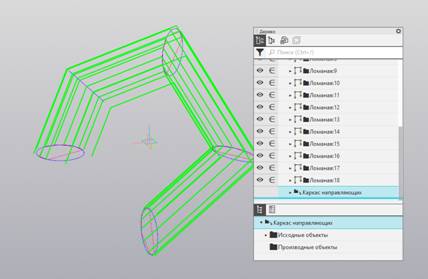
Рис. 5. Каркас направляющих ломаных

Замкнем ломаные каркаса (рис. 6).

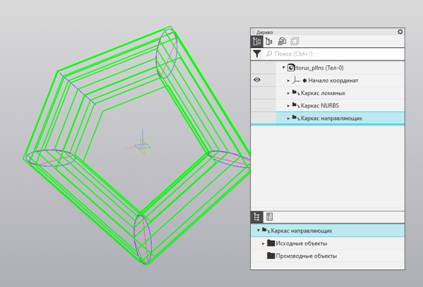
Рис. 6. Замкнутые направляющие ломаные.

Построим направляющие B-кривые поверхности на направляющих ломаных (рис. 7).

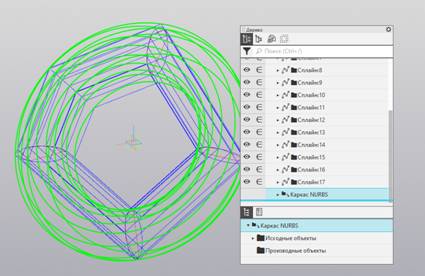
Рис. 7. Направляющие B-кривые поверхности.

По сути, поверхность готова. Осталось только определить фрейм поверхности на каркасе S-полигонов направляющих. Выделим в дереве построения каркас образующих NURBS кривых и затем каркас направляющих NURBS кривых. Сформируем поверхность (рис. 8) командой

Поверхности

1. Определить поверхность.

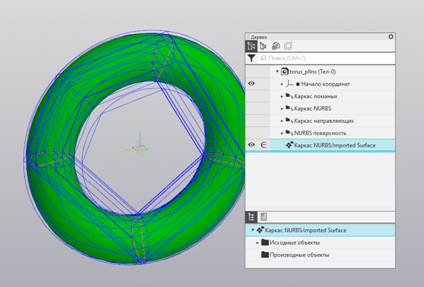
Рис. 8. B-поверхность степеней (8,8).

Поверхность определена во внутреннем формате прикладной библиотеки и используется для определения эквидистантной поверхности, нанесения рельефа на поверхность, аффинных преобразований поверхности.

Можно определить поверхность в формате штатного представления 'NURBS Surface' КОМПАС.

В папке C:/FairCurveModeler_Temp/Temp/ при выполнении команды 'Определить поверхность' формируется фрейм B-сплайновой поверхности. Этот фрейм сохраняется также в файле 'splv_name_spl.txt' в формате чтения из команды КОМПАС формирования NURBS поверхности на сети точек.

Для наглядности перейдите в новый файл

Выполните в КОМПАС команду построения NURBS поверхности на сети точек. Сеть точек прочитайте из файла C:/FairCurveModeler_Temp/Temp/splv_name_spl.txt.

При определении NURBS поверхности задавайте признаки замкнутости и порядки для образующих и направляющих кривых. Параметры NURBS поверхности можно узнать в текстовом файле '$attribsf.lst':

Образующие замкнуты, если u_bnd_st == 1, направляющие замкнуты, если v_bnd_st = 1.

Порядок образующих кривых = u_degree + 1, порядок направляющих кривых = v_degree + 1.

В данном случае задаются следующие параметры (рис. 9).

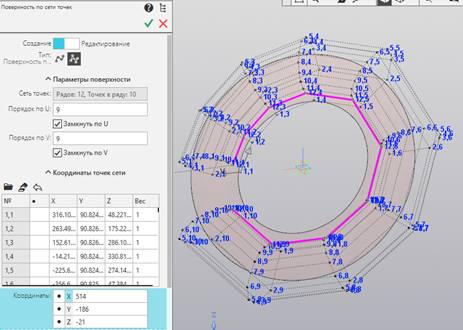
Рис. 9. Построение штатного примитива NURBS Surface КОМПАС.

Подтвердите построение (рис. 10).

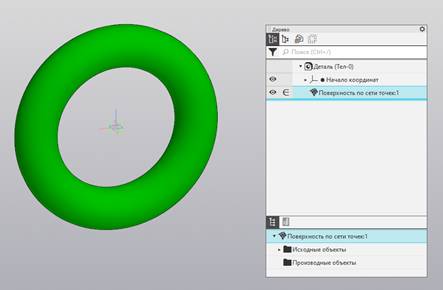
Рис. 10. Примитив NURBS Surface.

КОМПАС обладает уникальной возможностью представления замкнутой поверхности NURBS Surface как в закрытом формате (clamped), таки в открытом формате (float) (рис. ), который особенно удобен для редактирования замкнутых поверхностей на S-фрейме с обеспечением высокого порядка гладкости по швам сшивки поверхности в трансверсальном направлении (рис. 11).

Рис. 11. S-фрейм замкнутой поверхности в открытом формате.

Проверим точность построения.

Введем эскиз на плоскости, параллельной главной плоскости данной поверхности. Нарисуем окружности по центру и точкам на очерковых линиях поверхности. Визуально окружности совпадают с очерковыми линиями поверхности. Это говорит о высокой точности представления торовой поверхности посредством B-поверхности степеней 8*8 (рис. 12).

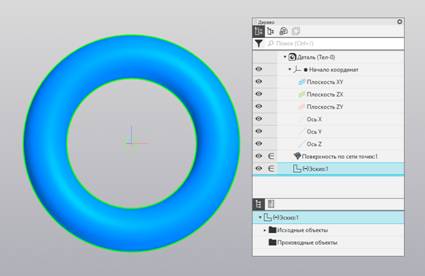
Рис. 12 NURBS поверхность порядков 9*9.

Исследуем качество поверхностей в системах визуализации. Приведем изображения к единому виду зрения (вид “Юго-Восточной”). На рис. 9 B-поверхность высоких степеней 8 * 8.

Рис. 13. B-поверхность степеней 8 * 8.

Построение в ‘Rhinoceros 3D’

Попробуем построить на тех же точках B-поверхность в CAD-системах, анонсирующих возможность построения кривых и поверхностей класса A.

Например, поверхность, построенная в ‘Rhinoceros 3D’ не обеспечивает даже достаточной точности представления торовой поверхности. Отклонения от формы тора фиксируются визуально (рис. 12, 13, 14).

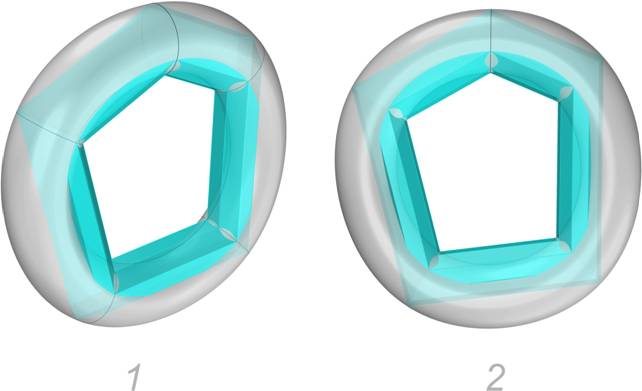
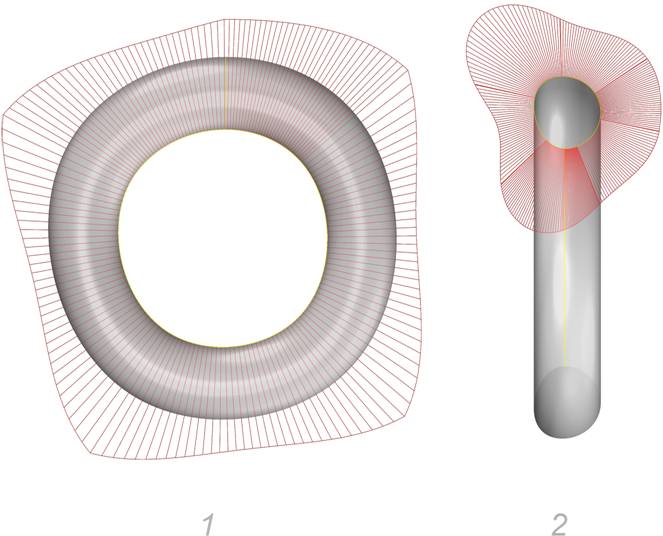
Рис. 12. B-поверхность степеней 8 * 8.

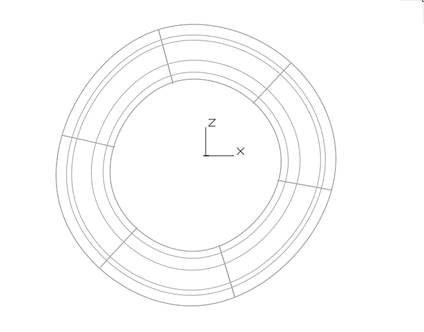
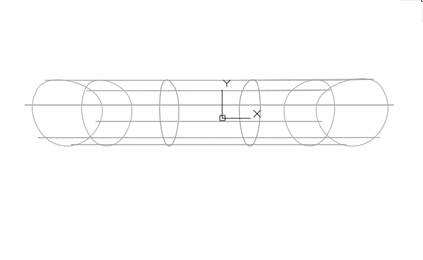
Рис. 13. Две проекции поверхности.

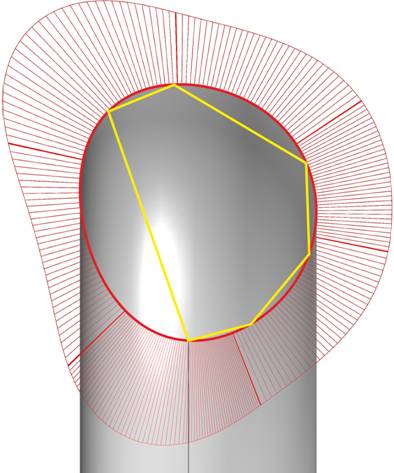
Рис. 14. График кривизны сечения.

Поверхность, построенная в ‘Rhinoceros 3D’ не обеспечивает достаточной точности представления торовой поверхности.

Хотя локальная плавность довольно приличная (рис. 15).

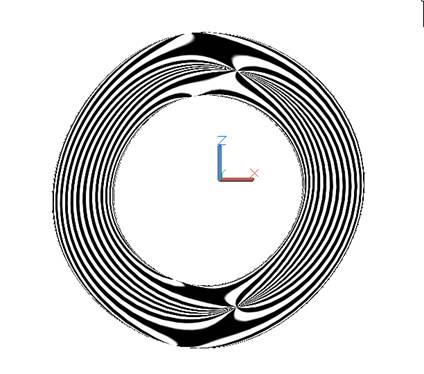
Рис. 15. Локальная плавность поверхности, смоделированной в ‘Rhinoceros 3D’.

Построение в «Alias AutoStudio 2024»

Рассмотрим пример построения на тех же точках в «Alias AutoStudio 2024» (рис. 16, 17, 18,19).

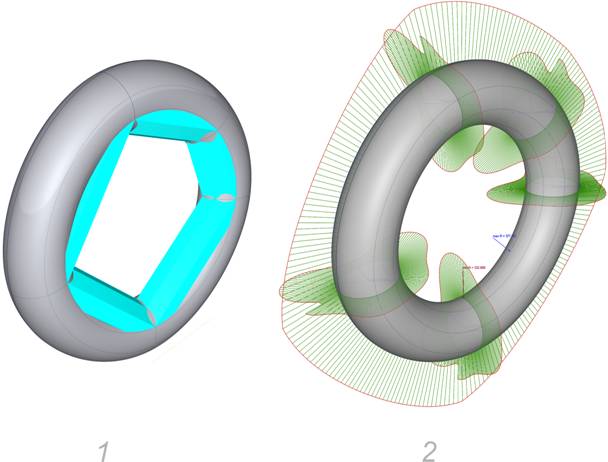
Рис. 16. Поверхность, построенная на точках тора в «Alias AutoStudio 2024».

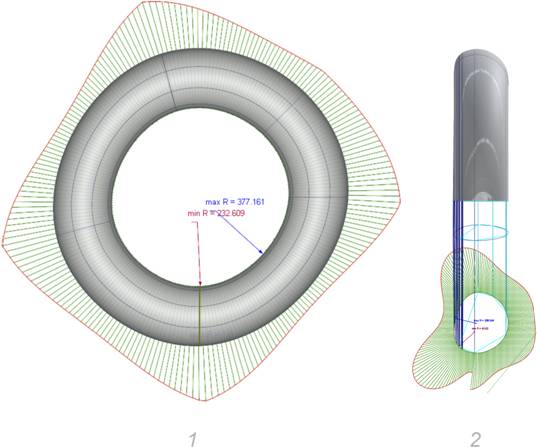
Рис. 17. Поверхность, построенная на точках тора в «Alias AutoStudio 2024».

Рис. 18. Поверхность, построенная на точках тора в «Alias AutoStudio 2024».

Рис. 19. “Зебра” также показывает недостаточную локальную плавность формы в «Alias AutoStudio 2024».

Качество поверхности, построенной в «Alias AutoStudio 2024», не соответствует классу F.

Выводы

1. Показана важность упреждающего внедрения инновационных методов геометрического ядра C3D + FairCurveModeler моделирования кривых и поверхностей класса А в образовательный процесс и в инженерную практику.

2. Поставлена и решена задача доработки прикладной библиотеки КОМПАС 3D на основе функционала C3D FairCurveModeler.

4. На ряде примеров моделирования кривых и поверхности показана технология моделирования в 'FairCurveModeler 3D.rtw’ КОМПАС 3D.

5. Проведено сравнение методов 'FairCurveModeler 3D.rtw’ КОМПАС 3D с методами Alias Design и Rhino. Показано бесспорное преимущество методов 'FairCurveModeler 3D.rtw’ КОМПАС 3Dм моделирования кривых и поверхностей класса F перед методами Alias Design и Rhino моделирования кривых и поверхностей класса A.

Литература

[1 Муфтеев & Максименко] Муфтеев В., Максименко А. Функциональные кривые высокого качества - инновация в геометрическом моделировании от C3D LABS // САПР и графика. 2021. № 5 (295). С. 62-72.

[2 Alias] Alias Design. https://www.autodesk.com/products/alias-products/overview?term=1-YEAR&tab=subscription&plc=ALSCPT

[3 Rhino]Rhino Ceros 3D. https://www.rhino3d.com/

[4 Фархутдинов 2012] Фархутдинов И.М. Совершенствование лемешно-отвальной поверхности корпуса плуга на основе моделирования технологического процесса вспашки. 05.20.01 — Технологии и средства механизации сельского хозяйства. Диссертация на соискание ученой степени канд. техн. наук. Научный руководитель доктор технических наук профессор С.Г. Мударисов. Уфа, 2012. -138 с.

[5 2021] Прикладные САПР и приложения на основе геометрического ядра C3D для проектирования изделий с функциональными кривыми / В.Г. Муфтеев, А. Максименко, Р.И. Ахметшин, А.П. Зелев, Р.А. Зиатдинов, Ф.Т. Зиганшина, Р.И., Набиев, И.М. Фархутдинов, М.М. Фаттахов // GraphiCon 2021. Геометрическое моделирование. Компьютерная графика в образовании. С. 75-87.

[6 2022 Приложения] FairCurveModeler 3D прикладная библиотека КОМПАС 3D. http://spliner.ru/HELP.html

[7 Сергин Р.П.] Сергин, Р. П. Технология нурбс-моделирования и анимация биоморфных

объектов / Р. П. Сергин // Современные тенденции компьютерного проектирования орнамента : сборник материалов Всероссийского Круглого стола с международным участием, Москва, 25 октября 2023 года. - Москва: Федеральное государственное бюджетное образовательное учреждение высшего образования ’’Российский государственный университет имени А.Н. Косыгина (Технологии. Дизайн. Искусство)”, 2023. - С. 175-181. - EDN NZJSAS.

[8 Farin] Farin G. NURB Curves and Surfaces from Projective Geometry to Practical Use. (A. K. Peters,1995).

[9 Мерседес-Бенц] Шпур Г., Ф.-Л. Краузе. Автоматизированное проектирование в машиностроении/Пер. с нем. Г. Д. Волковой и др.; Под ред. Ю. М. Соломенцева, В. П. Диденко. — М.: Машиностроение, 1988. —648 с.: ил.

[10 Учебник] Промышленный дизайн: учебник / М.С. Кухта, В.И. Куманин, М.Л. Соколова, М.Г. Гольдшмидт; под ред. И.В. Голубятникова, М.С. Кухты; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2013. – 312 с