FairCurveModeler
Описание
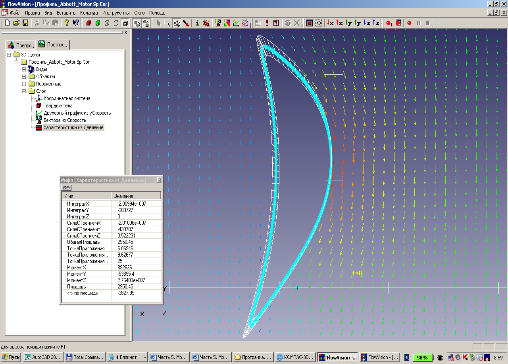
Приложение FaiCurveModeler app (ZWCAD, BricsCAD, AutoCAD) для геометрического моделирования изделий с функциональными кривыми и поверхностями. Приложение реализовано на основе инновационного раздела FaiCurveModeler геометрического ядра C3D. Приложение реализует весь функционал раздела C3D©FairCurveModeler. И в этом смысле является полноценным его представителем. Приложение FaiCurveModeler предназначено для геометрического моделирования изделий с функциональными кривыми и поверхностями. Геометрические параметры функциональных поверхностей являются определяющими для функциональных характеристик проектируемого объекта в целом. Применение методов C3D©FairCurveModeler позволяет получить кривые высочайшего качества (класса F): высокого порядка гладкости (до 9-го порядка), с минимальным количеством экстремумов кривизны, с плавным изменением кривизны с ограниченной вариацией и с ограничением на скорость изменения, с плавным кручением пространственной кривой. Прежде всего, приложения FairCurveModeler предлагается пользователям специализированных CAD-систем, производители которых декларируют возможность моделирования кривых линий и поверхностей высокого качества. Этим пользователям действительно нужны функции моделирования кривых линий и поверхностей высокого качества. И такую функциональность, но обеспечивающую более высокое качество кривых и поверхностей, они найдут в приложении FairCurveModeler (see curves comparison FairCurveModeler vs NX and 'Alias Design Studio') and (see comparison of surfaces FairCurveModeler vs NX, Rhinoceros 3D and Alias Design Studio) Вторая группа пользователей, которым нужна функциональность приложений FairCurveModeler, - это пользователи, которые обходятся в проектировании стандартными машиностроительными CAD-системами, но которые хотели бы улучшить потребительские свойства проектируемых изделий высококачественными по функциональности и эстетике геометрическими формами (see the examples of analyzis and of improving primitive _Helix in ZWCAD). Третья группа - пользователи графических пакетов (например, Corel Draw) и анимационных программ (например, 3D MAX Studio) - дизайнеры, художники, web-дизайнеры, геймеры, аниматоры, которым нужно нарисовать просто красивую линию, красивую поверхность с использованием удобных, наглядных и точных видов геометрических определителей (see the examples of modeling and editing curves in the application) Геометрия различных изделий формообразуется функциональными кривыми и поверхностями: 1) профиль крыла самолета / профиль лопатки турбины создает подъемную силу. При моделировании кривой профиля необходимо максимизировать подъемную силу при минимизации лобового сопротивления. Предложенные техники моделирования на основе метода Abbott’а, но с применением кривых класса F, позволяют существенно улучшить аэродинамические характеристики стандартных профилей ЦАГИ, NACA и профилей лопаток турбин и компрессоров. Сравнительное тестирование исходных профилей и улучшенных профилей в системе FlowVision показывает значительное повышение аэродинамического качества улучшенных профилей.
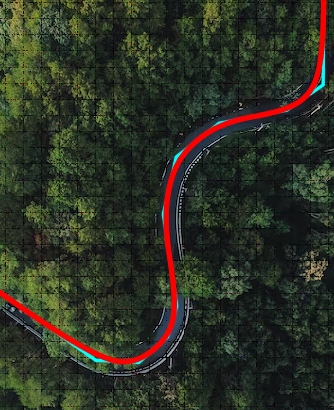
2) трасса дороги должна обеспечивать комфортную безопасную езду на транспортном средстве, поэтому необходимо добиваться максимальной плавности трассы при заданных ограничениях. Уникальные функции C3D FairCurveModeler построения кривых на касательной ломаной позволяют проектировать трассу дороги, заданную ломаной теодолитных ходов, с высоким качеством плавности и с минимизацией длины трассы и ее потенциальной энергии
3) профиль кулачка определяет перемещение толкателя с клапаном для обеспечения необходимого закона газораспределения, поэтому при его конструировании рекомендуется добиваться безударного плавного движения клапана. Предложенные техники моделирования в приложении позволяют обеспечить гладкость 9-го порядка! интегральной кривой с точными дугами окружностей верхнего и нижнего “выстоя”.
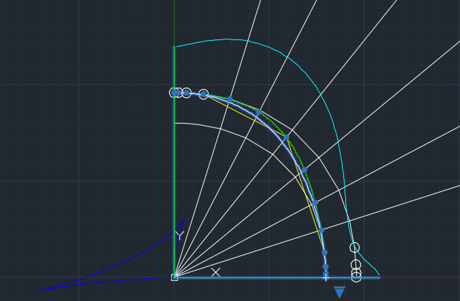
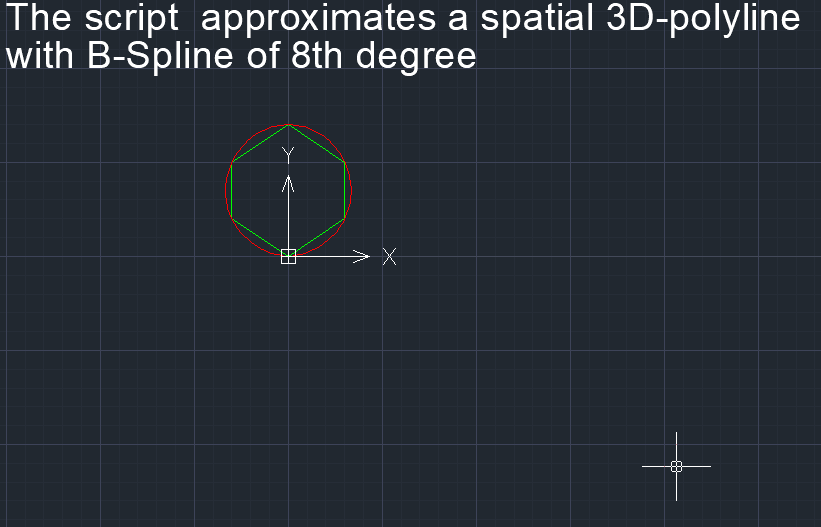
Переходный участок между участками выстоя в виде NURBzS кривой 8-ой степени. Обеспечивается 7-ой порядок гладкости.
4) среди функциональных кривых можно выделить подкласс инженерных аналитических кривых, которые единственным оптимальным образом обеспечивают проектную характеристику объекта. К таким кривым, например, можно отнести эвольвенту окружности, используемую для построения профиля зубьев зубчатого колеса, а также брахистохрону — кривую наискорейшего спуска для транспортировки предметов. Цепная линия, используемая для моделирования поверхности купола или висячей конструкции, а также клотоида, используемая для конструирования участков виража с линейным изменением центробежной силы, начиная с нуля, — все это тоже примеры инженерных аналитических кривых. Предложенные техники аппроксимации в приложении позволяют изогеометрически (с сохранением формы и базовых свойств) аппроксимировать аналитические кривые.
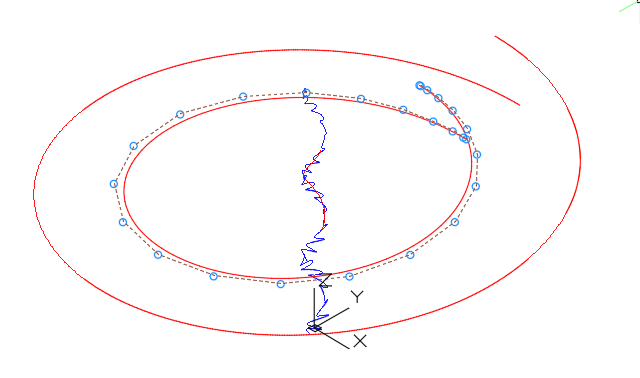
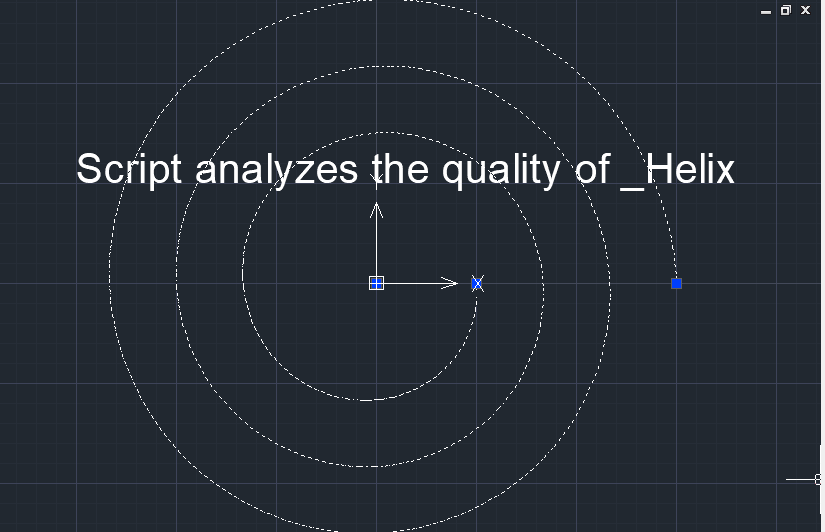
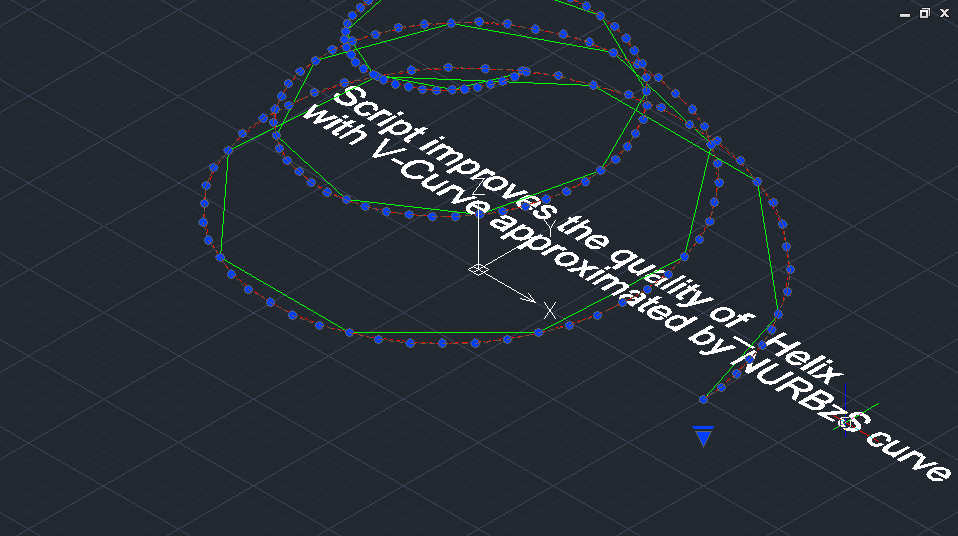
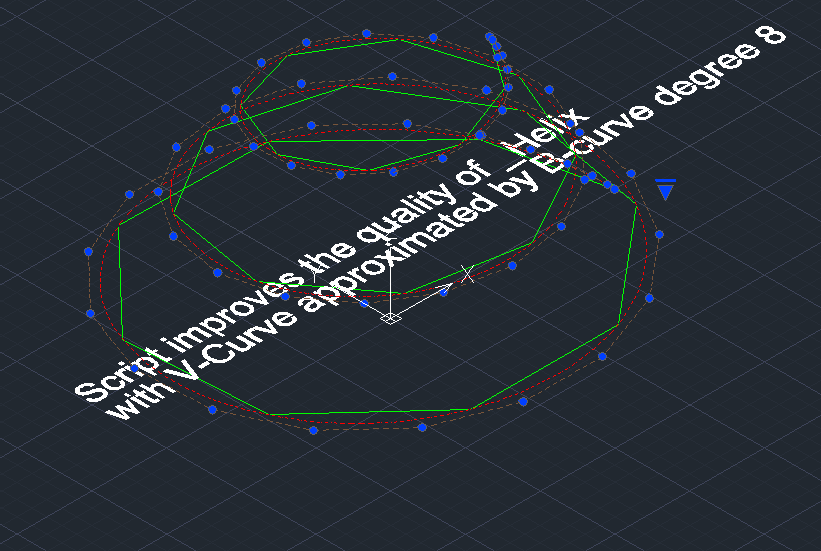
Аппроксимация B-сплайновой кривой степени 8 точек примитива _Helix AutoCAD. Идеальные эпюра кривизны и эволюта B-сплайновой кривой (показаны красным цветом). Эволюта штатного примитива _Helix AutoCAD показана синим цветом.
5) в промышленном дизайне / в инженерных задачах часто требуется построение кривых с монотонной кривизной. Кроме команд аппроксимации фиксированных аналитических кривых в приложении можно использовать три дополнительные команды построения эстетических кривых:
- начального участка клотоиды с заданием длины и конечной кривизны;
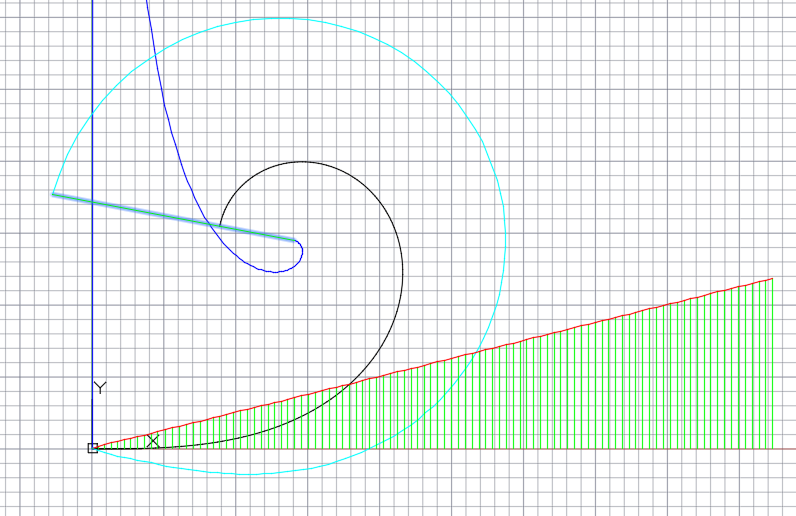
- сектрисы Маклорена – участка кривой с монотонной кривизной, заданного соприкасающимся треугольником;
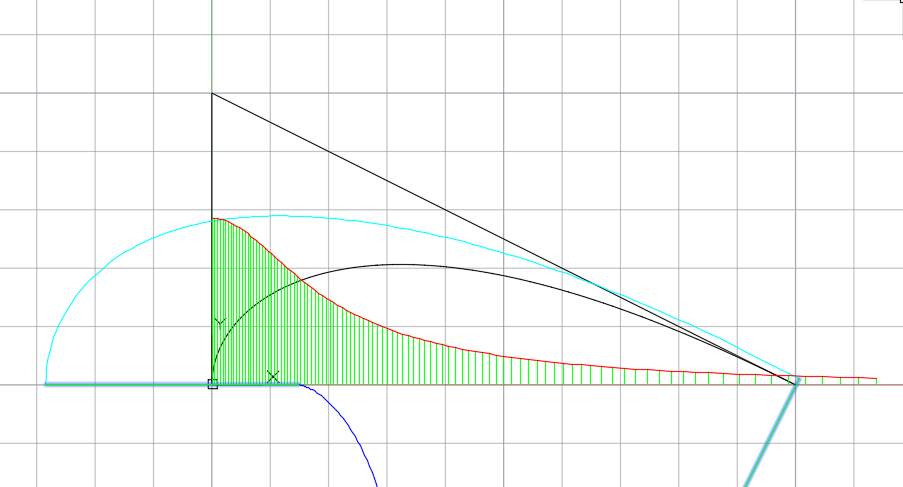
- участка B-сплайновой кривой с монотонной кривизной путем генерации вершин открытого S-полигона с заданным коэффициентом удлинения звеньев и фиксированным углом между звеньями.
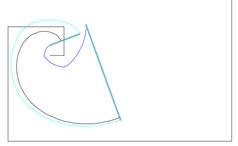
Участок B-сплайновой кривой 4-ой степени с монотонной кривизной (коэффициент удлинения 2, угол 90 градусов).
Замена в стандартной конструкции плуга направляющей кривой вида параболы посредством участка клотоиды с теми же макропараметрами позволила получить потрясающий результат: повысилось качество вспашки и уменьшилась энергоемкость обработки.
6) в реверсивном инжиниринге возникает проблема аппроксимации кривой, заданной массивом “зашумленных” точек. Точная интерполяция приводит к кривой с осцилляцией кривизны. Команды FairCurveModeler построения сглаживающих кривых решают данную проблему.
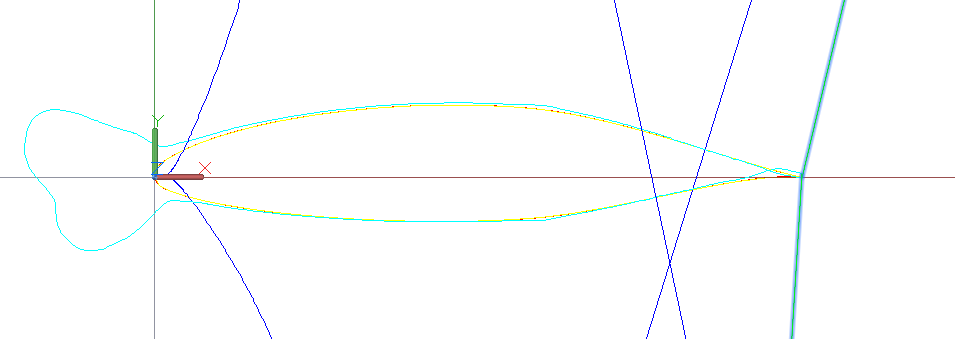
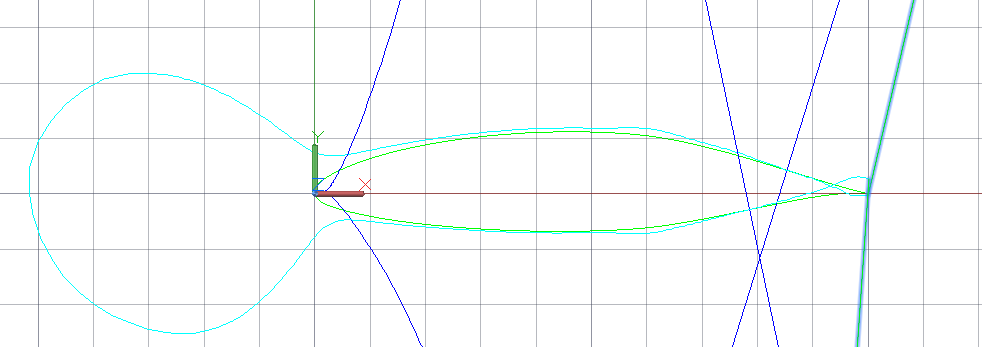
Рис. До и после сглаживания.
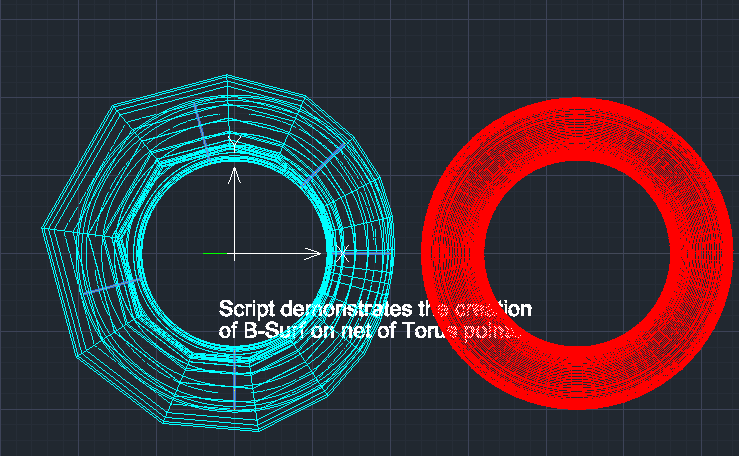
7) в приложении реализованы команды построения B-сплайновых поверхностей. Разработан каркасно-кинематический способ представления B-сплайновой поверхности произвольного формата. Построение каркасно-кинематической B-сплайновой поверхности делится на 2 этапа:
Первый этап — построение образующих B-сплайновых кривых класса F.
Второй этап — построение направляющих B-сплайновых кривых класса F на столбцах сети S-полигонов образующих кривых.
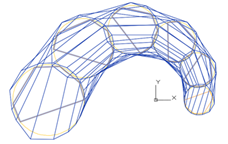
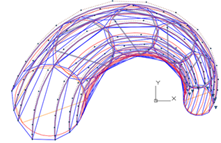
Каркас S-полигонов направляющих B-сплайновых кривых формирует S-фрейм B-сплайновой поверхности.
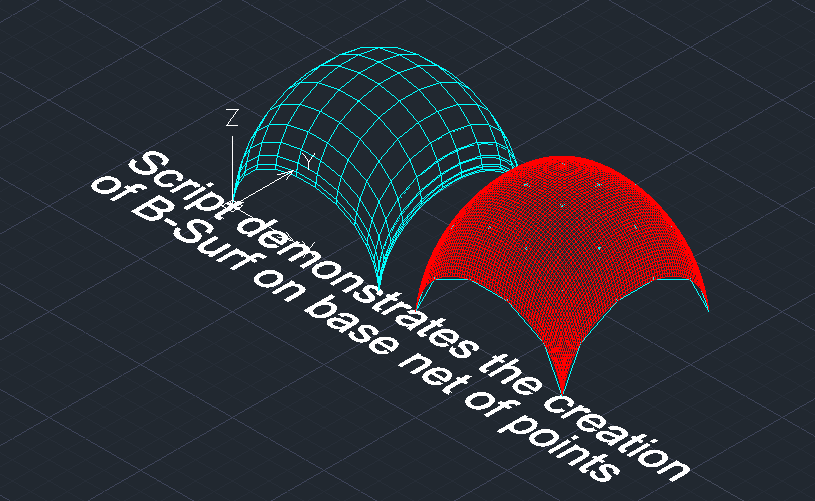
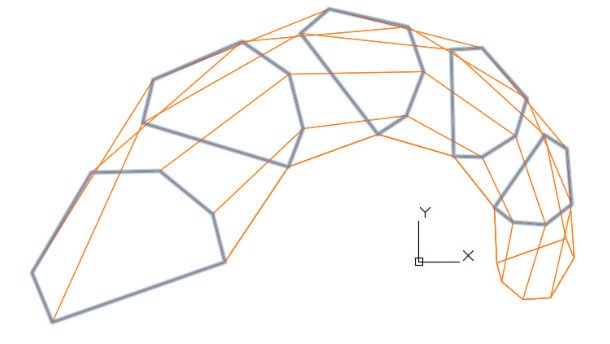
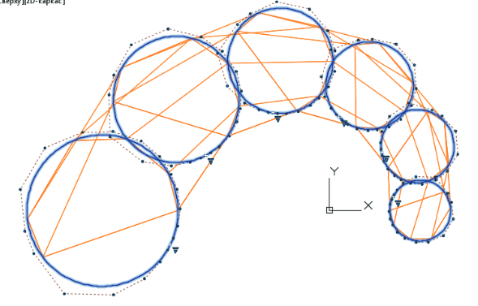
8) применение опции построения образующих и направляющих поверхности на касательной позволяет конструировать поверхности, касательные к исходному многограннику из сети точек. Это может быть полезным при свободном конструировании изделий промышленного дизайна. В этом случае как бы задается массив материала и, чтобы получить шедевр, по выражению Микеланджело, “убирается все лишнее”.
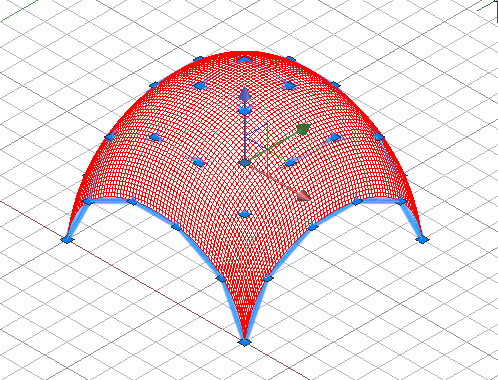
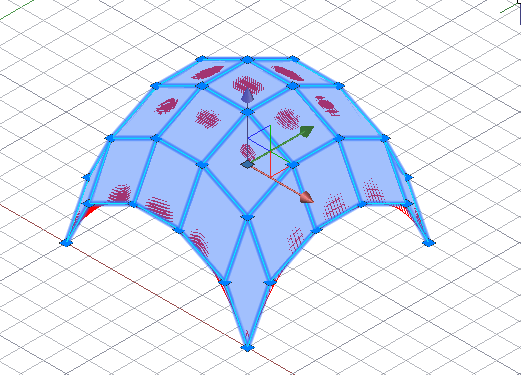
Построение поверхности на опорной сети и на касательной сети.
9) внешнюю кузовную поверхность автомобиля, архитектурные криволинейные формы здания, формы изделий промышленного дизайна можно отнести к функциональным поверхностям, если эстетичность и красоту рассматривать как проектную характеристику изделия, которая определяет его потребительские свойства. Чрезвычайно важно отсутствие осцилляции изопараметрических кривых поверхности. Наличие осциллирующих изопараметрических кривых приводит к эффекту “кривых зеркал”. Предложенные техники моделирования в приложении позволяют устранить осциллирующие изопараметрические кривые на проекции.
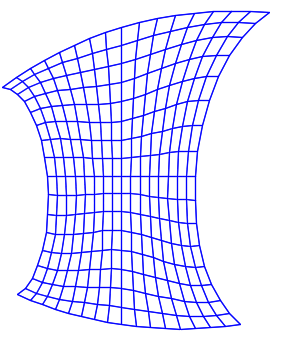
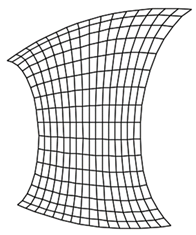

До исправления и после исправления.
Применение FairCurveModeler – это
простой, быстрый и дешевый способ улучшения качества изделия!
Общие инструкции по использованию
Команда V_Model это основная команда Приложения. Команда создает плавные кривые и поверхности. Команда имеет сложную структуру опций вида строкового меню. Конкретный набор опций зависит от выбранного объекта:
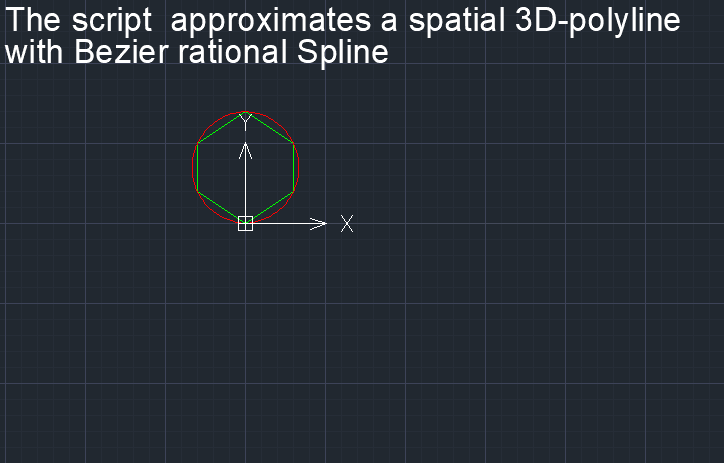
1) 3D полилиния - используется для редактирования и создания плавной V-кривой и аппроксимации созданной V-кривой посредством рациональной сплайновой кривой Безье (NURBzS) кривой или B-кривой. 3D полилиния может быть использована в качестве опорной ломаной или касательной ломаной и может быть использована непосредственно в качестве S-полигонов B-сплайновой кривой. Набор 3D полилиний может быть объединена в полигональную сеть 3D Mesh для построения B-поверхности.
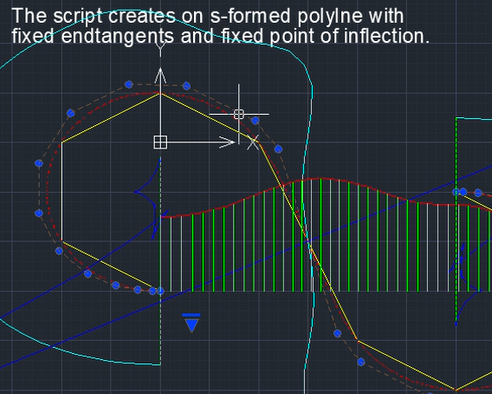
2) ГО Эрмита - представляется в виде примитива '3D-полилиния'. 3D-полилиния обходит опорные точки, касательные векторы, векторы кривизны в следующей последовательности: опрная точка > конец вектора касательной > возврат к опорной точке > конец вектора кривизны > возврат к опорной точке > переход к следующей опрной точке > ... Таким образом 3D полилиния полностью обеспечивает информацию о параметрах ГО Эрмита 2-го порядка фиксации. Можно редактировать ГО Эрмита стандартными средствами CAD-системы, сохраняя структуру ГО. Можно напрямую строить NURBzS кривую на ГО Эрмита 2-го порядка фиксации. Можно напрямую строить B-кривую на ГО Эрмита 1-го порядка фиксации. На опорной ломаной ГО Эрмита или на касательных ГО Эрмита можно строить V-кривые с аппроксимацией посредством NURBzS-кривых или B-кривых. Параметры ГО в концевых точках и в точках перегиба можно использовать при построении V-кривой. Методы построения V-кривой позволяют также фиксировать заданные направления касательных ГО Эрмита. Подробнее .
3) NURBzS кривая (созданная на 3D полилинии или на ГО Эрмита) - это стандартная форма представления сплайна в Autodesk® AutoCAD®.
4) NURBS кривая (созданная непосредственно на 3D полилинии или ГО Эрмита) - это стандартная форма представления сплайна в AutoCAD. NURBS кривая может быть отредактирована посредством S-полигона с тестированием качества по графикам кривизны и эволюты.
5) 3D Mesh - полигональная сеть используется: - для создания образующих плавных V-кривых на строках и аппроксимация посредством B-сплайновых кривых, затем для построения B-сплайновых кривых на столбцах 3D Mesh S-полигонов образующих B-сплайновых кривых. И на каркасе направляющих B-сплайновых кривых создать B-сплайновую поверхность (NURBS поверхность).
6) Каркас B-кривых используется для построения B-сплайновых направляющих. Представляется полигональной сетью, составленной из S-полигонов B-кривых. На столбцах 3D Сети S-полигонов строятся B-сплайновые направляющие кривые для создания B-сплайновой поверхности (NURBS поверхности).
7) NURBS поверхность создается на каркасе направляющих B-кривых в Приложении. Вы можете проверить качество поверхности, создать параллельные поверхности. Чтобы перевести NURBS поверхности Приложения в примитивы AutoCAD, Вы должны поверхности Приложения конвертировать геометрически точно через IGS-формат в NURBS поверхности AutoCAD. Вы можете редактировать B-сплайновую поверхность посредством s-фрейма с тестированием качества и с управлением формы произвольной изопараметрической кривой.
8) Две дополнительные команды (V_Aesthetic, V_Hermite) предназначены для моделирования эстетических и инженерных кривых на базе аналитических кривых. При проектировании изделий промдизайна и изделий с функциональными кривыми часто требуются кривые с определенными свойствами: эстетические кривые с монотонным изменением кривизны (клотоида и сектриса Маклорена), цепная линия для моделирования куполов или висячих конструкций; линия наискорейшего спуска для синхронизации времени движения частиц под действием силы тяжести из любой точки кривой до конечной точки; та же клотоида с линейным изменением кривизны для трассировки дороги; и т.д. Приложение позволяет использование различных аналитических кривых. Пример.
Приложение не позволяет тестировать и редактировать непосредственно сплайновые полилинии. Предварительно преобразуйте сплайновые полилинии в реальные NURBS кривые: Command:_Spline > Object > Выберите сплайновые полилинии.
Команды
| Значок | Команда | Описание команды |
|---|---|---|

|
Строит кривые и поверхности высокого качества по критериям плавности. |
|

|
Строит участки клотоиды, сектрисы Маклорена, "типической кривой". |
|

|
Строит NURBS кривые на основе аналитических кривых, заданных таблицей координат точек, векторов касательных и значений кривизны.Предварительно подготовьте таблицу параметров аналитической кривой в MathCAD Лабораторная работа. Подготовка NURBS шаблонов аналитических кривых для CAD-систем |
Правила / Ограничения
Приложение FairCurveModeler является специализированным приложением САПР и предназначено для геометрического моделирования функциональных кривых. Качество функциональных кривых напрямую определяют качество проектируемых изделий в авиастроении, судостроении, автомобилестроении, двигателестроении и во многих других отраслях.
Существуют инвариантные, относительно специфики отраслей, требования к качеству функциональных кривых: - высокий порядок гладкости; - минимальное число экстремумов кривизны; - плавность графика кривизны / ограничение на скорость изменения кривизны; - плавность кручения пространственной кривой; - ограничения на максимальное значения кривизны; - малое значение потенциальной энергии.
Геометрическое моделирование функциональных кривых выполняется на этапе эскизного проектирования изделия. На этапе эскизного проектирования определяется теоретический чертеж / теоретическая геометрическая модель изделия. Соответственно, теоретический чертеж кривой или теоретическая модель кривой.
Цена ошибки или некачественного построения функциональных кривых может быть очень большой и стоить больших денег в этих отраслях. И это чревато не только потерей денег, но и потерей конкурентоспособности. Предлагаемые правила и ограничения при построении моделей кривых позволяют гарантировать высокое качество моделируемых кривых и, соответственно, высокое качество изделия.
Модель кривой строится на основе дискретной модели кривой, т.н. геометрического определителя (ГО). В приложении FairCurveModeler используются три вида ГО: опорная ломаная, касательная ломаная для определения плоской кривой, ГО Эрмита.ГО Эрмита - это опорная ломаная, оснащенная во всех вершинах касательными векторами [и векторами кривизны]. Для определения пространственных кривых вместо касательной ломаной используется ГО Эрмита, оснащенный в вершинах ломаной только векторами касательных. Это ГО Эрмита первого порядка фиксации. В общем случае точки и касательные векторы пространственной ломаной определяют скрещивающиеся прямые.
Опорная ломаная может оснащаться в концевых вершинах касательными векторами и векторами кривизны и в отдельных вершинах фиксированными касательными векторами. Касательная ломаная или ГО Эрмита первого порядка фиксации может оснащаться векторами кривизны в концевых вершинах и фиксированными точками на касательных прямых. Кроме геометрических параметров вида ломаной, векторов касательных и векторов кривизны ГО может содержать дополнительные параметры вида условий и ограничений (определенный порядок гладкости, допустимые максимальные значения кривизны и скорости изменения кривизны).
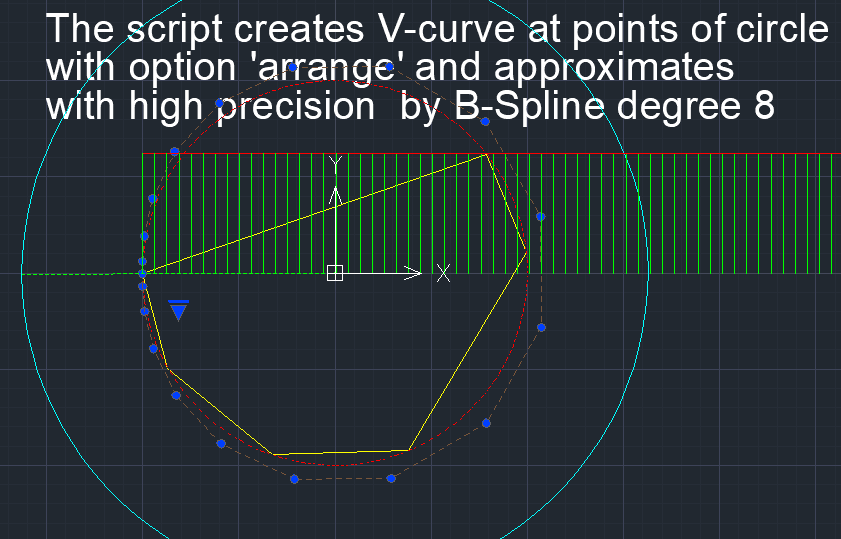
Полная геометрическая модель кривой (Определитель кривой) содержит ГО + методы построения кривой на ГО. В системе FairCurveModeler это методы построения т.н. виртуальной кривой (V-кривой) высокого качества по критериям плавности и изогеометрическая аппроксимация V-кривой посредством B-сплайновой кривой или рациональной сплайновой кривой Безье (NURBzS кривой).
В процессе геометрического моделирования кривых должны соблюдаться метрологические требования. Прежде всего, должна обеспечиваться метрологическая определенность. Все требуемые свойства функциональной кривой должны быть заданы в структуре ГО и аппроксимирующая кривая должна обладать именно этими свойствами.
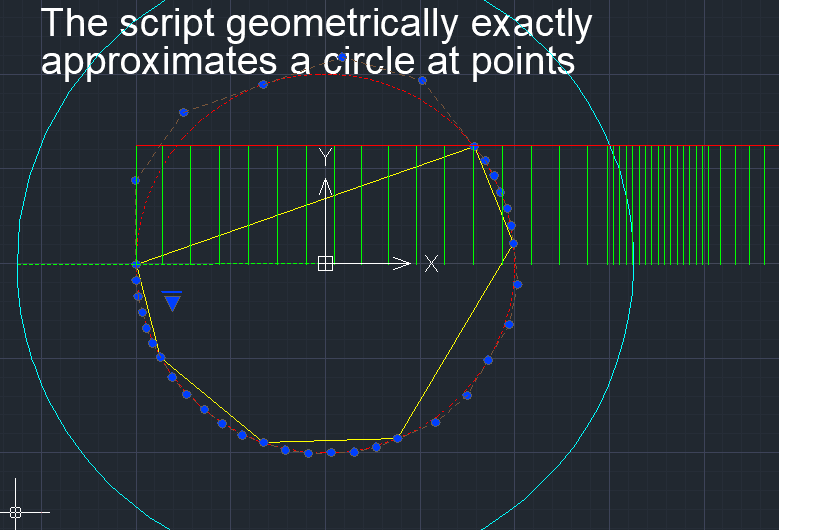
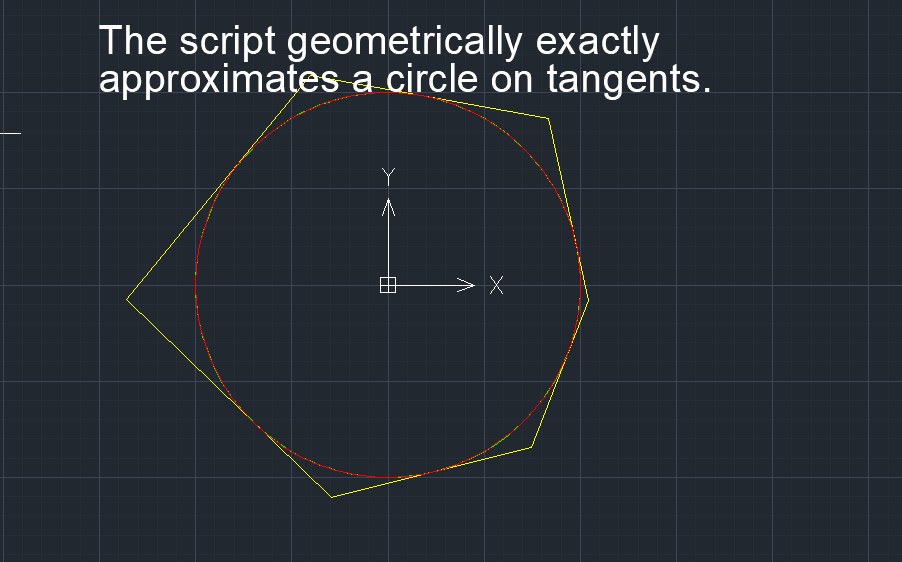
В системе FairCurveModeler метрологическая определенность обеспечивается строгим изоморфизмом (изогеометричностью) структуры кривой и структуры ГО. Форма кривой и ее параметры однозначно определяются формой и параметрами ГО. То есть ГО 1) позиционирует кривую на ГО с точным прохождением кривой через вершины опорной ломаной / с касанием звеньев плоской касательной ломаной / с касанием касательных прямых пространственного ГО; 2) определяет форму с точностью до количества точек перегиба (количества локально выпуклых участков); 3) определяет на кривой участки монотонного изменения кривизны.
Определитель кривой с доведенным до кондиций метрологичности ГО обеспечивает высокое качество кривой по критериям, приведенным выше. Для доведения ГО до кондиции метрологической определенности используются уникальные методы системы FairCurveModeler: сглаживания, репараметризации и гармонизации.
Для обеспечения метрологической определенности приняты определенные правила оформления опорной / касательной ломаной. В парадигме "с самого начала" (ab-initio) или "с чистого листа" (tabula rasa) конструктор может начинать готовить ГО по правилам построения регулярной ломаной. Регулярная ломаная оформляется по следующим правилам. Углы между звеньями > 90, прямолинейные участки кривой задаются вершинами на прямой. Выразительность формы обеспечивается ограничением на минимальную стрелку прогиба, ограничением на разницу длин смежных звеньев. Оснащение ГО дополнительными параметрами вида фиксированных касательных на опорной ломаной или фиксированных точек на касательной ломаной не должно противоречить форме контрольной ломаной. Фиксированные точки должны иметь свободные от фиксации смежные точки.
Эти правила и ограничения обеспечивают возможность однозначного задания формы кривой. То есть обеспечивают метрологическую определенность задания формы кривой.
Однако для задания кривой с участками монотонного изменения кривизны требуется уметь формировать ломаные гармоничной формы. Гармоничная форма ломаной это такая форма ломаной, при которой вершины ломаной распределяются по контуру ломаной с плотностью пропорциональной кривизне. При этом график дискретной аппроксимации кривизны по длине ломаной однозначно определяет график кривизны аппроксимирующей кривой.
В системе FairCurveModeler для построения ломаной гармоничной формы конструктор может использовать в системе различные приемы: - формировать т.н. типические ломаные (команда genFrame ) - брать точки с аналитических кривых с монотонной кривизной ( Clothoid или Sectrix ). - выполнить команду гармонизации исходной регулярной ломаной ( gaRmonize ). Гармонизированная ломаная однозначно определяет участки кривой с монотонным изменением кривизны.
Не всегда конструктор работает в парадигме "с чистого листа". Для эскизирования кривой могут быть предоставлены измеренные данные со сканера или данные из таблиц бумажного чертежа, которые представляют собой зашумленные данные. Последовательность приведения этих данных к теоретическому чертежу с метрологической определенностью следующая: 1) Выполняется команда onMiddleLine сглаживания по средней линии. Предварительно на измеренных данных рисуется черновая опорная ломаная. Затем указывается ломаная зашумленных точек. Алгоритм команды сглаживания на опорной ломаной строит кривую и затем эту кривую деформирует таким образом, чтобы сумма отклонений зашумленных точек "слева" от кривой была равна сумме отклонений "справа". То есть полученная кривая является средней линией относительно зашумленных точек. 2) Полученная сглаженная кривая репараметризуется Transform > Reparam. При этом узлы репараметризованной кривой гармонично перераспределяются по контуру кривой. 3) Снимается ГО с репараметризованной кривой Transform > toHermite. 4) ГО сглаживается в заданном коридоре OnCoridor . При этом качество кривой улучшается. При сглаживании с этой опцией плавность кривой улучшается.
Доведенный до кондиции метрологической определенности ГО + варианты аппроксимирующих кривых и есть метрологически определенный Определитель кривой. При этом в ГО кривой содержатся все параметры для контроля качества кривой на всех этапах проектирования, испытаний и производства изделия.
Установка / Удаление
Разархивируйте на C:/ с опцией "в текущую папку" FairCurveModeler.zip Должны возникнуть две папки: c:/FairCurveModeler c:/FairCurveModeler_TEMP Запустите c:/FairCurveModeler/Exec/WebFairCurveExe.exe от имени администратора. Подтвердите регистрацию в реестре. Запустите ZWCAD / BricsCAD / AutoCAD. Загрузите в ZWCAD / BricsCAD / AutoCAD приложения из папки c:/FairCurveModeler/Lisp/ LISP_C3DFCModeler_Com.lsp s_init_zwcad.lsp Создайте новый чертеж. Используйте скрипты в папке Scripts для 1) проверки работоспособности приложения; 2) для обучения. Вызов справочной информации в CAD-системе: V_Help_Ru Вызов справок из папок c:/FairCurveModeler/Help_RU/Help_Ru.html Начните выполнять команды самостоятельно.
Удаление приложения От имени администратора выполните c:/FairCurveModeler/Exec/v_unreg.bat Удалите папки c:/FairCurveModeler c:/FairCurveModeler_TEMP