Моделирование и реконструкция моделей аэродинамических профилей
Муфтеев В.Г., Марданов А.Р. (БГАУ) и др.
(статья к публикации) 

Аннотация
В статье рассматривается метод v-кривых (виртуальных кривых) для моделирования выпуклых кривых 5-го порядка гладкости с плавным изменением кривизны. Описывается авторская программа FairCurveModeler, разработанная на основе метода v-кривых, моделирования плоских и пространственных кривых произвольной формы высокого качества по критериям плавности. Анализируется специализированный метод Abbott’а моделирования аэродинамического профиля. Показывается влияние геометрического качества профиля на динамические характеристики крыла. Предлагается модификация метода Abbott’а для моделирования аэродинамических профилей высокого качества и метод реконструкции существующих профилей по методу Abbott’а с использованием программы FairCurveModeler. 

Введение
В работе [Муфтеев В.Г. , 1980 1] был предложен метод моделирования выпуклых кривых 5-го порядка гладкости. Моделируемая кривая является огибающей непрерывного семейства дважды соприкасающихся К2П. Кривая огибающая названа виртуальной кривой или v-кривой [Муфтеев В.Г., 2]. Через 15 лет после публикации метода чрезвычайно близкий метод был предложен в 1995 математиком R.W. Soanes из US ARMY Benet Laboratories [Royce W. Soanes 1995 3]. На основе базового метода [1] и методов [2, 4, 5, 6], обобщающих и развивающих базовый метод, разработана авторская программа FairCurveModeler для моделирования плоских и пространственных кривых произвольной формы с плавным изменением кривизны.
В статье анализируется специализированный метод Abbott’а моделирования аэродинамического профиля. Показывается влияние геометрического качества профиля на динамические характеристики крыла. Предлагается модификация метода Abbott’а для моделирования аэродинамических профилей высокого качества, и метод реконструкции существующих профилей с использованием программы FairCurveModeler.
Перечень команд и опций программы FairCurveModeler, используемых при моделировании и реконструкции аэродинамических профилей
Команда V_Model – вызывает программу FairCurveModeler.
Setvar (установить параметры) – устанавливает тип геометрического определителя (Incpllne – опорная ломаная/Tngpllne – касательная ломаная/Splframe - сплайновый фрейм).
Splframe (установить сплайновый фрейм) – устанавливает ломаную как управляющую ломаную сплайновой кривой. Опция Degree – задает степень кривой. Опция Format – определяет тип кривой (сплайновая кривая Безье, b-сплайновая кривая, кривая Безье).
Curvatre (задать кривизну) – задает значение кривизны в конечных точках кривой.
Edvrtxs (редактировать вершины) – редактирует геометрический определитель с контролем графика кривизны. Опция incRmove – перемещает точку в инкрементальном режиме путем задания направления (setDir) и шага (setStep). Опция Del – удаляет текущую точку ломаной).
Crtscrv (создать кривую) – создает v-кривую в формате кубического NURBzS шаблона.
Функция FrenchCurve (лекальная кривая) – создает кубический NURBzS шаблон кривой, заданной списками точек, касательных векторов, значений кривизны.
Multiply (уплотнить) - уплотняет спецификацию геометрического определителя кривой.
Команда V_Test (тестировать кривую) – выводит графики кривизны указанной кривой. Можно указать любой криволинейный примитив (NURBS кривые, дуги окружностей и эллипсов, спираль). 

Метод моделирования семейства профилей крыла NACA – 4 – digit
Рассмотрим возможности использования v-кривой в прикладной программе САПР на примере моделирования семейства профилей крыла NACA – 4 – digit методом Abbott’а [Boehm, 7] .
Аналитическая кривая Безье z(t) 8-ой степени с управляющей ломаной {(0., 0.) , (0.,0.18556), (0.03571 0.34863),(0.10714 0.48919), (0.21429 0.58214),(0.35714, 0.55724), (0.53571, 0.44929),(0.75000, 0.30281), (1.00000, 0.01050)} используется для аппроксимации некоторого симметричного эталонного профиля z(t), 0 <= t <= 1 (рис. 1).


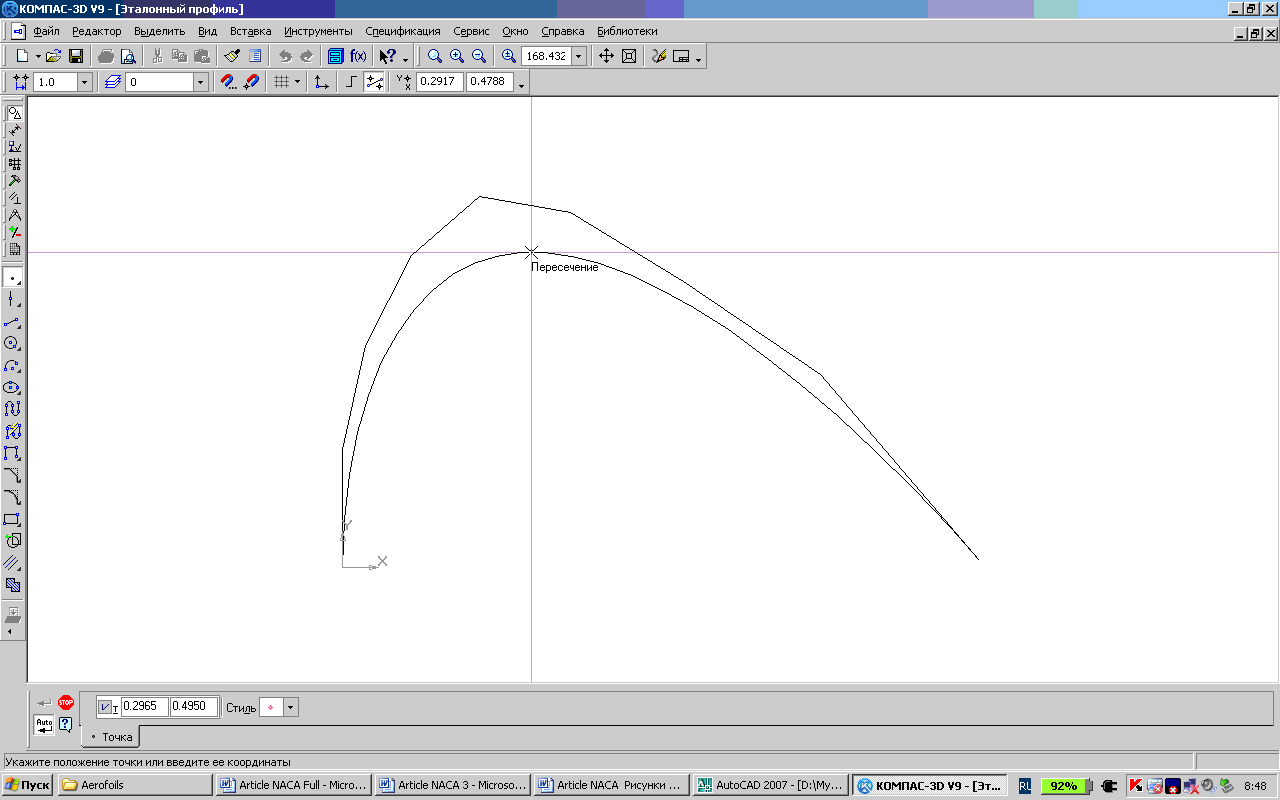
Рис. 1. Эталонный профиль – кривая Безье 8-ой степени. 

Профиль z(t) имеет максимальное утолщение в точке (0.2965,0.4950). Отметим, что построение прямой, касательной к кривой Безье, невозможно выполнить в AutoCAD, но можно выполнить в КОМПАС (см. рис. 1).
Сплайновая кривая Безье 2-ой степени 1-го порядка гладкости с управляющими точками {(0.,0.), (p*/2,m*) , (p*,m*) , ((p*+1)/2, m*) , (1.,0.)} используется для построения средней линии профиля крыла m(x), 0 < x < 1, x = t?. Конкретные значения параметров m*, p*, q* определяют конкретный профиль семейства. Параметр q* определяет амплитуду профиля. Радиус закругления r профиля определяется параметром q*: r = 1.1019•(q*)? .
Собственно профиль крыла p(x) получается отображением симметричного профиля z(t) на среднюю линию m(x) профиля крыла. Точки симметричного эталонного профиля z(t) откладываются по нормалям n(x) к средней линии m(x): p(x) = m(x) ± n(x)•z(t)•q*. То есть используется суперпозиция функций. Здесь отметим, что порядок гладкости результирующей кривой совпадает с наименьшим порядком гладкости функции, входящей в суперпозицию. В данном случае гладкость профиля крыла p(x) будет 1-го порядка гладкости. Это существенный недостаток способа.
Проф. Boehm в статье [7] предлагает 2 варианта улучшения метода. Исходную кривую Безье 8-ой степени z(t), аппроксимирующую симметричный профиль NAСA, он предлагает:
1) заменить сплайновой кривой Безье 3-ей степени, обосновывая необходимость замены большей распространенностью метода (“Composite Bezier curves of lower degree will be used”);
2) заменить кубической сплайновой кривой и затем перейти к представлению сплайновой кривой Безье.
По нашему мнению, замена аналитической кривой составной кривой 1-го порядка гладкости, как в 1-ом варианте, и кривой 2-го порядка гладкости, как во 2-ом варианте, только ухудшит геометрическое качество профиля по критериям плавности.
Для моделирования аэродинамических профилей была написана авторская прикладная программа V_Abbott на AutoLISP, реализующая метод Abbott’а [Boehm, 7] в среде AutoCAD (Приложение П1). Функция Abbott_Profile на основе кривой Безье 8-ой степени формирует точки симметричного эталонного профиля и от точек средней линии (любая кривая - примитив AutoCAD) по нормали вверх и вниз откладывает ординаты точек симметричного контура, формируя контур профиля. Затем по точкам контура строит сплайн (примитив SPLINE). Функция Param_Abbott запрашивает примитив для средней линии, параметр масштабирования (q*) ординат эталонного профиля z(t) и количество точек контура. Вызов программы, осуществляется командой V_Abbott. Программа V_Abbott использует также функции, написанные на AutoLISP, геометрического ядра программы FairCurveModeler. Поэтому предварительно загружается программа FairCurveModeler.
По методу Abbott’а формируется средняя линия по значениям m* = 0.1, p* = 0.4, q* = 0.3 как сплайновая кривая Безье 2-ой степени. Управляющая ломаная сплайновой кривой Безье 2-ой степени представляет последовательность точек {x,y} = {(0.,0.), (0.2,0.1) , (0.4,0.1) , (0.7,0.1) , (1.,0.)}. С помощью команды Crtscrv (при значениях опций Splframe = 1, Format = 3, Order 2) определим сплайновую кривую Безье 2-ой степени из двух сегментов. Протестируем качество кривой (команда V_Test) (рис. 2, а).
Отработаем программу V_Abbott для построения профиля, указав сформированную среднюю линию, задав коэффициент масштабирования (q* = 0.3) и количество точек 100. Командой V_Test выведем график кривизны примитива SPLINE, построенного на точках профиля в программе V_Abbott. График кривизны имеет особенность в районе участка стыка сегментов средней линии (см. рис. 2, а).



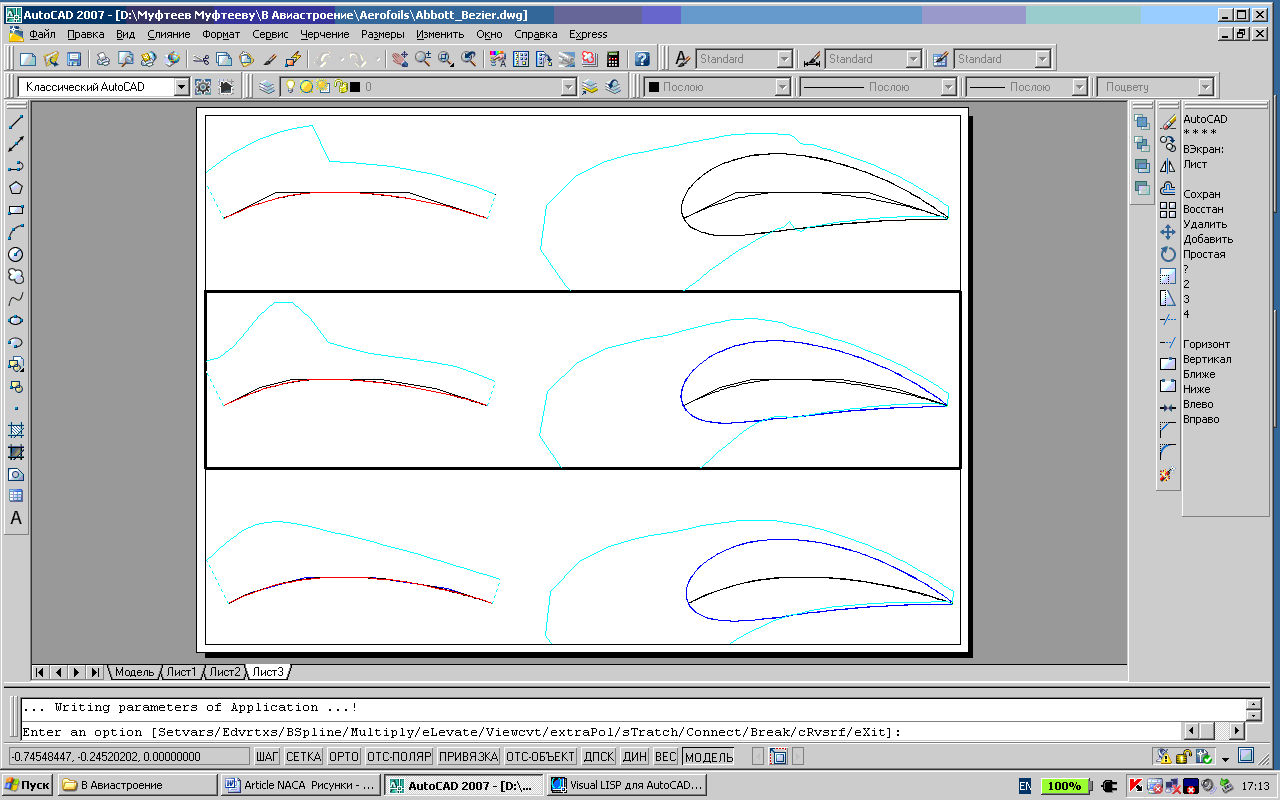
Рис. 2. Моделирование аэродинамического профиля по методу Abbott’а: а) средняя линия - сплайновая кривая Безье 2-ой степени; б) средняя линия – “лекальная кривая”; в) средняя линия - v-кривая.

Для устранения данного недостатка программу FairCurveModeler можно применить непосредственно в прикладном алгоритме для аппроксимации и улучшения средней линии профиля.

Улучшим геометрические характеристики средней линии с помощью программы FairCurveModeler, сохраняя макропараметры средней линии метода Abbott’а - касательные и значения кривизны в граничных точках, касательную прямую в средней точке.

1) Используем метод лекальной кривой.
Для формирования средней линии написана программа на AutoLISP MeanCurve c вызовом функции формирования лекальной кривой (FranceCurve xyz dxyz cvt). Для формирования лекальной кривой программой подготавливаются списки с координатами точек xyz = ((0.0 0.0 0.0) (0.4 0.1 0.0) (1.0 0.0 0.0)), касательных векторов dxyz = ((0.894427 0.447214 0.0) (0.3 0.0 0.0) (0.948683 -0.316228 0.0)) и кривизны cvt = (0.894427 0.684384 0.474342). В средней точке значение кривизны берется равной средней арифметической от значений кривизны в граничных точках, направление касательной сохраняется. Построенный кубический NURBzS шаблон лекальной кривой представляет следующую последовательность управляющих точек с весовыми коэффициентами {x, y, w} = {(0.0, 0.0, 1.0),(0.139815, 0.0699074, 1.00359), (0.260185, 0.1, 1.22676), (0.4, 0.1,1.0), (0.596497, 0.1, 0.933083), (0.803503, 0.065499, 1.00026), (1.0, 0.0, 1.0) }.
Лекальная кривая обеспечивает непрерывность кривизны средней линии и профиля (рис. 1, б)

2) Используем метод v-кривой на геометрическом определителе вида касательной ломаной.
Подготовим геометрический определитель. Уплотним исходный геометрический определитель шаблона лекальной кривой, сплайновой NURBzS кривой 3-ей степени, (команда V_Model > укажем сплайновую кривую > опция Multiply). Уплотнение даст управляющую ломаную сплайновой кривой с 4-мя сегментами. Разобьем определитель на составляющие ломаные – ломаную управляющих точек и ломаную интерполяционных точек кривой (опция Break). И используем управляющую ломаную точек как геометрический определитель v-кривой в виде касательной ломаной. Касательная ломаная позволит сохранить более точно основные параметры средней линии.
Выполним команду V_Model > укажем ломаную. В опции Setvar установим тип Tngpllne геометрического определителя в виде касательной ломаной. В опции Curvatre в начальной точке зададим кривизну 0.894427, в последней точке кривизну 0.474342. Перейдем к редактированию (опция Edvrtxs). Удалим (опция Del) средние точки на отрезках (точки стыка сегментов сплайновой кривой Безье). Получим касательную ломаную { x, y } = {( 0.0, 0.0) ( 0.086271594442754, 0.043135797221990) (0.291194045149939, 0.1)( 0.545447971388546, 0.1) ( 0.830481346363127, 0.056506217878383 )( 1.0, 0.)}

Опцией Crtscrv построим на касательной ломаной v-кривую.
Кубический NURBzS шаблон v-кривой представляет следующую последовательность точек с весовыми коэффициентами {x, y, w } = {(0.0, 0.0,, 1.0) (0.0576662, 0.0288331, 1.0022)(0.114182, 0.0508807, 1.00842) (0.170447, 0.0664938, 1.0) (0.251351, 0.088944, 1.01606) (0.339236, 0.1, 1.00437), (0.436789, 0.1, 1.0) (0.509127, 0.1, 0.997133) (0.585455, 0.0938953, 0.997262)(0.665132, 0.0817371, 1.0) (0.77438, 0.0650668, 0.986643) (0.887997, 0.0373343, 0.978265) (1.0, 0.0, 1.0)}.
Отработаем программу V_Abbott для построения профиля, указав сформированную среднюю линию, задав коэффициент масштабирования 0.3 и количество точек 100. На, построенном на точках профиля, примитиве SPLINE сформируем график кривизны (рис. 2, в)
Как видим, при сохранении исходных геометрических макропараметров, кроме положения средней точки, мы получили более качественный по критериям плавности аэродинамический профиль.
Средняя точка сместилась от значения x=0.4 до значения x=0.436789.

Проведем сравнительные испытания профилей в аэродинамической трубе, имитируемой в системе Flow Vision.
Геометрическая модель – аэродинамическая труба прямоугольного сечения размером 10?10?1 м, прямоугольное крыло с длиной хорды профиля – 1м, с углом атаки – 0 градусов. Нулевая точка профиля помещена в точку (5,5) на плоскости XY. Граничные условия на профиле – (Стенка, логарифмический закон), на стенках аэродинамической трубы - (Симметрия, Стенка с проскальзыванием)), на входе аэродинамической трубы - граничное условие входа с нормальной скоростью V=100м/с и нулевым давлением (Вход/Выход, Нормальная скорость с давлением), на выходе аэродинамической трубы – граничное условие свободного выхода (Свободный выход, Свободная граница).
Физические параметры (Начальные значения) - начальное распределение скорости в области 100 м/с. Расчетная сетка 100?100?1, шаг по времени 0.001 с.
Модель – несжимаемая жидкость. Вещество – воздух.
На рис. 3, 4 показаны результаты испытания крыла прототипа с профилем Abbott’а на средней линии – квадратичной кривой Безье (см. рис. 2,а). На рис. 3 показан график скоростей по направлению X на прямой проходящей параллельно хорде крыла над верхней точкой утолщения максимального утолщения. Максимальная скорость – 146.741 м/сек.


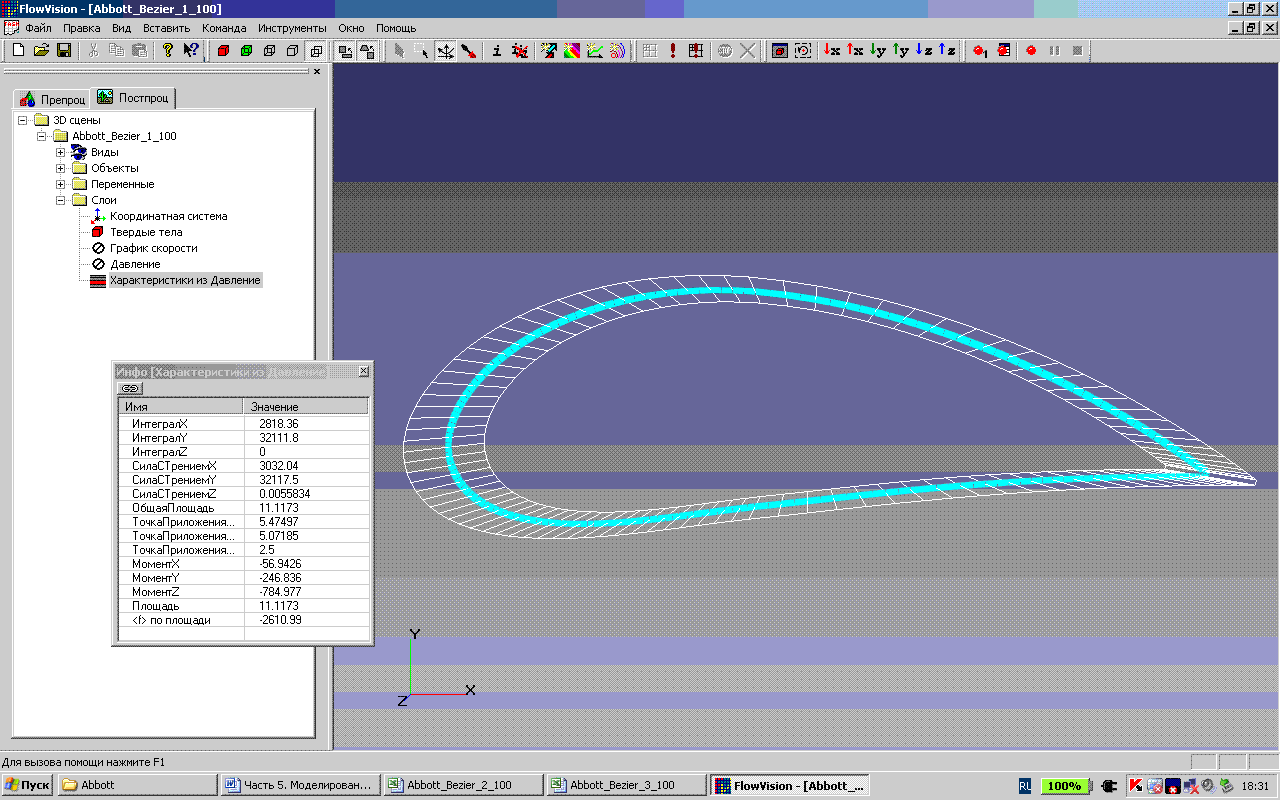
Рис. 3. Распределение скорости (XСкорость) на прямой, проходящей над верхней точкой утолщения профиля прототипа.



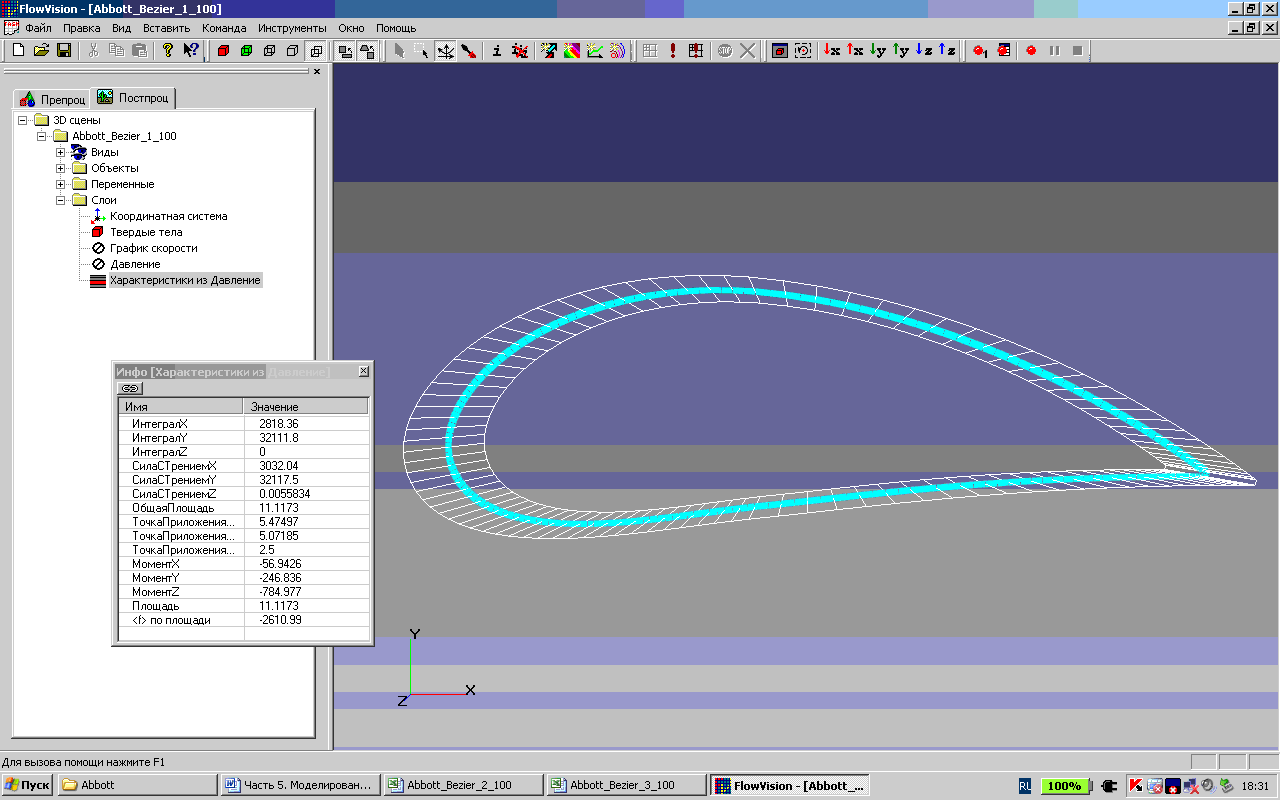
Рис. 4. Вывод интегральной характеристики крыла – давления.

На рис. 4 показано окно вывода интегральной характеристики крыла – давления. Компоненты интегральной характеристики имеют следующие значения СилаСТрениемХ = 3032.04, СилаСТрениемY = 32117.05, ТочкаПриложенияМоментаX = 5.47497, ТочкаПриложенияМоментаY = 5.07185. Аэродинамическое качество крыла СилаСТрениемY/ СилаСТрениемХ = 10.5926.
Для улучшенных профилей были получены следующие результаты.
1) Крыло с профилем Abbott’а на средней линии – лекальной кривой (см. рис 2, б).
Компоненты интегральной характеристики имеют следующие значения: СилаСТрениемХ = 2628.33, СилаСТрениемY = 29177.4, ТочкаПриложенияМоментаX = 5.4767, ТочкаПриложенияМоментаY = 5.06683. Максимальная скорость по направлению X – 158.11 м/сек. Аэродинамическое качество крыла СилаСТрениемY/ СилаСТрениемХ = 11.1011.
Повышение качества геометрических характеристик профиля Abbott’а (см. рис. 2, б), определенной на средней линии –лекальной кривой 2-го порядка гладкости, улучшило аэродинамические характеристики крыла.
Крыло имеет меньшее (на 15.36%) лобовое сопротивление при несколько уменьшенной (на 10.07 %) подъемной силе. Точки приложения сил практически не изменились.
Аэродинамическое качество крыла повысилось (на 4.80%).


2) Крыло с профилем Abbott’а на средней линии – v-кривой (см. рис 2, в).
Компоненты интегральной характеристики имеют следующие значения СилаСТрениемХ = 2376.07, СилаСТрениемY = 32625.8, ТочкаПриложенияМоментаX = 5.47517, ТочкаПриложенияМоментаY = 5.07184. Максимальная скорость по направлению X – 148.253 (рис. 5). Аэродинамическое качество крыла СилаСТрениемY/ СилаСТрениемХ = 13.731.


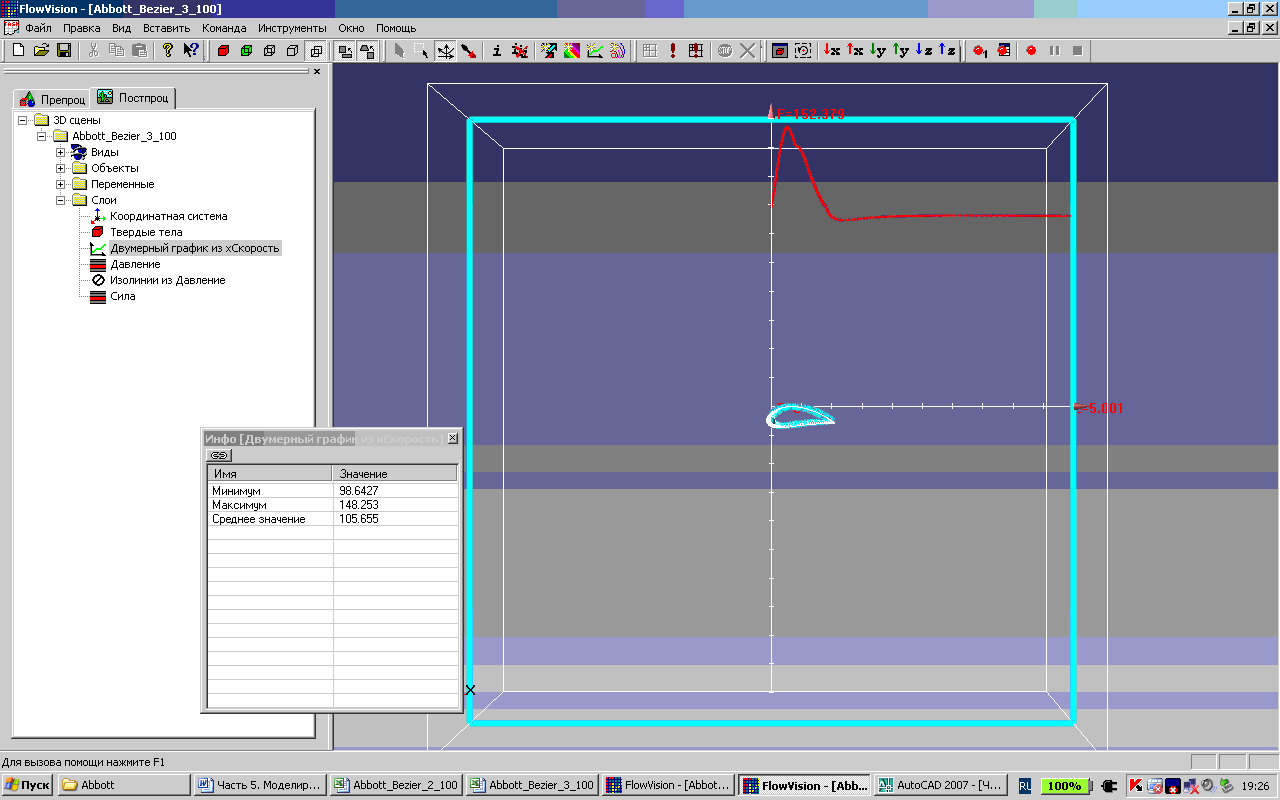
Рис. 5. Распределение скорости (XСкорость) на прямой, проходящей над верхней точкой утолщения профиля Abbott’а на средней линии – v-кривой.

Повышение качества геометрических характеристик профиля Abbott’а (см. рис. 2, в), определенной на средней линии – v-кривой 5-го порядка гладкости с плавным изменением кривизны, значительно улучшило аэродинамические характеристики крыла.
Крыло имеет меньшее (на 21.63%) лобовое сопротивление при увеличенной (на 1.58 %) подъемной силе. Точки приложения сил практически не изменились.
Аэродинамическое качество крыла повысилось (на 29.6%).

Реконструкция и модификация аэродинамического профиля по методу Abbott’а

Для реконструкции и модификации аэродинамических профилей была написана прикладная программа V_Abbott_Re на AutoLISP (Приложение П2). Функция Abbott_Profile_Re на основе точек профиля формирует точки средней линии и точки эталонного профиля.
С помощью программы FairCurveModeler ломаная средней линии профиля аппроксимируется v-кривой. Редактированием v-кривой можно модифицировать среднюю линию.
Затем программой V_Abbott строится модифицированный профиль.
Рассмотрим предложенный способ реконструкции на примере реконструкции профиля NACA 4412 [Атлас профилей NACA, 8]. Координаты профиля вводятся с помощью script-файла (П3).
С помощью программы V_Abbott_Re реконструируем ломаные средней линии и эталонного профиля (рис. 6).


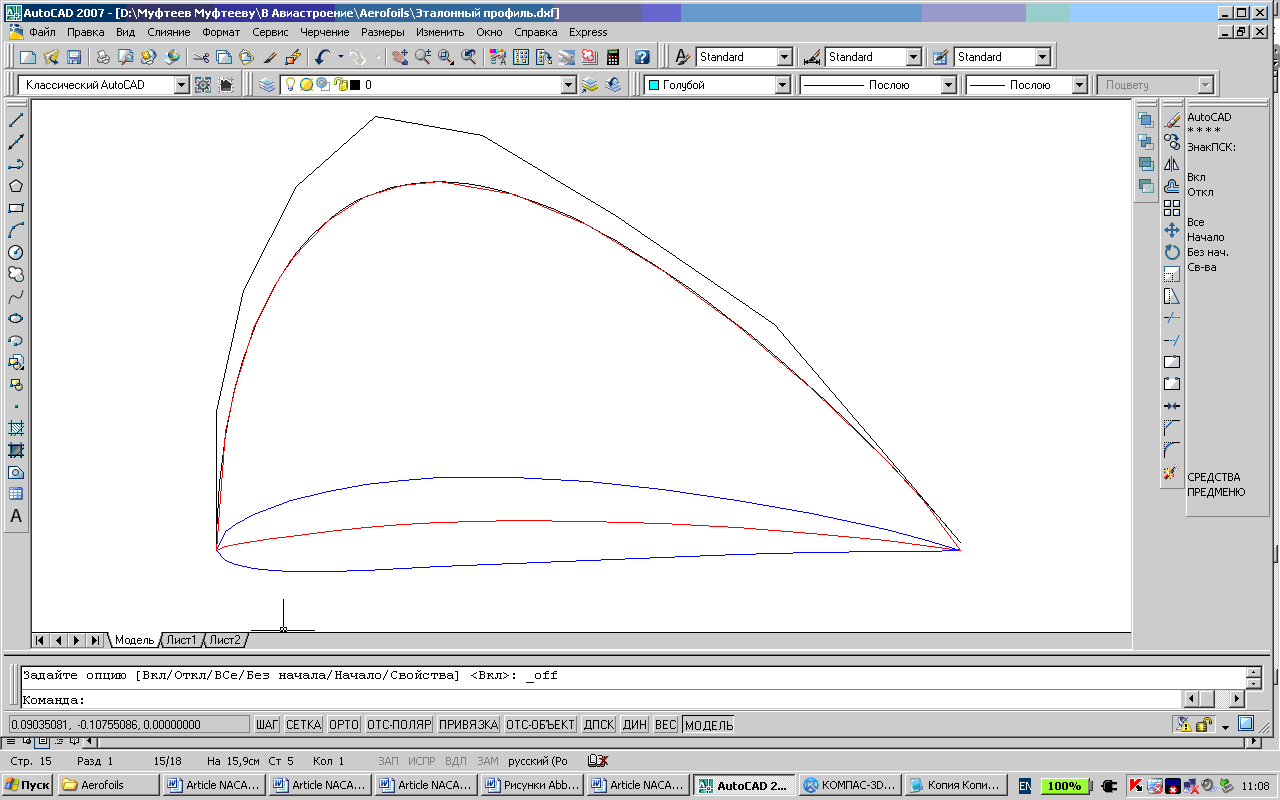
Рис. 6. Реконструкция средней линии и эталонного профиля NACA 4412

Ломаная точек эталонного профиля NACA 4412 совпадает с эталонным профилем метода Abbott’а, после масштабирования ломаной для приведения максимальной толщины профилей к одному значению (рис. 8), кроме конечной точки. Отредактируем эталонную функцию z(t) для более точной аппроксимации ломаной точек эталонного профиля NACA 4412. Управляющая ломаная кривой Безье 8-ой степени, аппроксимирующей эталонный профиль NACA 4412 представит последовательность {(0., 0.) , (0.,0.18556), (0.03571 0.34863),(0.10714 0.48919), (0.21429 0.58214),(0.35714, 0.55724), (0.53571, 0.44929),(0.75000, 0.30281), (1.0, 0.0)}.

Для реконструкции профиля построим v-кривую, точно аппроксимирующую среднюю линию профиля NACA 4412 по точкам ломаной средней линии профиля NACA. Затем программой V_Abbott, указав v-кривую средней линии, количество точек 200, коэффициент масштабирования 0.121414 и способ откладывания (0) ординат профиля от средней линии, построим точки профиля NACA 4412 (рис. 9).



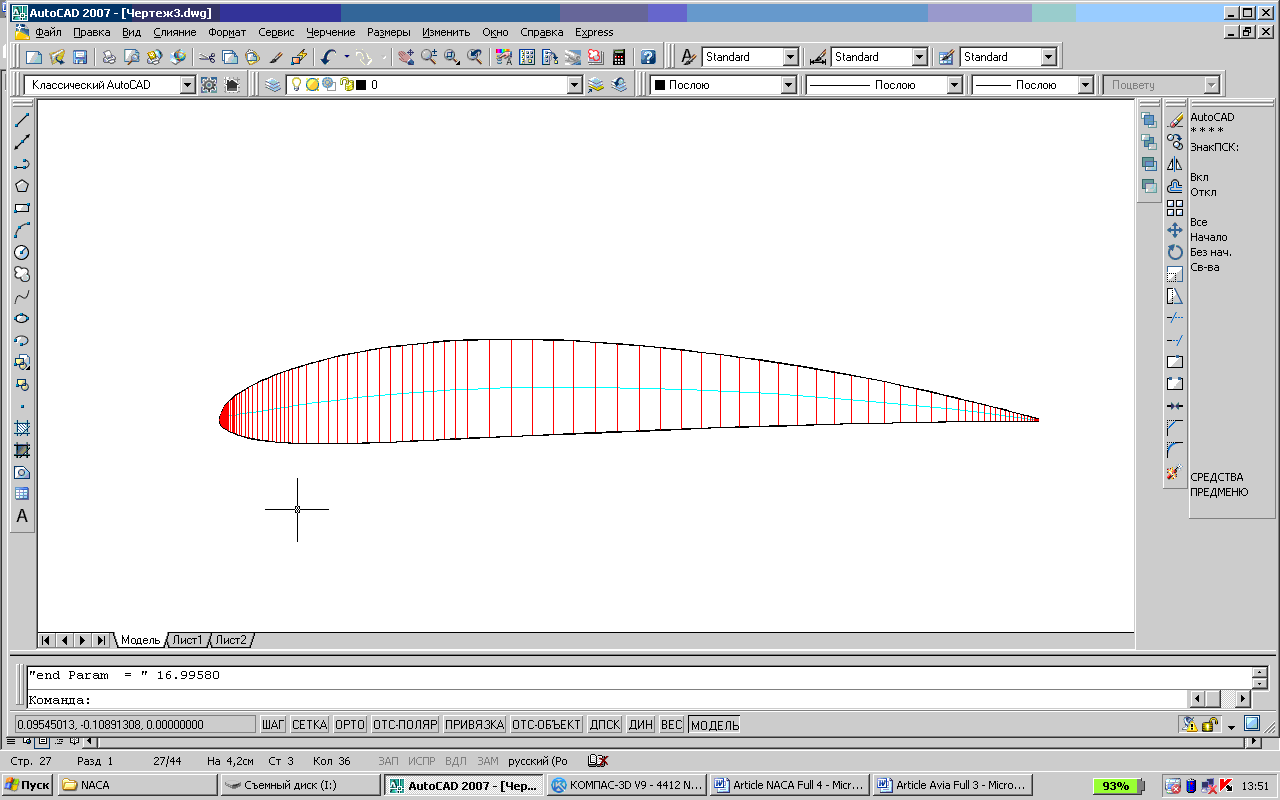
Риc. 7. Реконструкция профиля NACA 4412.

Метод позволяет реконструировать профили NACA с произвольным количеством точек.


Заключение
В статье дан анализ специализированного метода Abbott’а моделирования аэродинамического профиля. Показано влияние геометрического качества профиля на динамические характеристики крыла.
Предложена модификация метода Abbott’а для моделирования аэродинамических профилей высокого качества с использованием программы FairCurveModeler. Использование v-кривой для аппроксимации средней линии профиля позволяет улучшить геометрические характеристики профиля и, как следствие, существенно улучшить аэродинамическое качество профиля. Применение геометрического определителя v-кривой вида касательной ломаной позволяет сохранять исходные макропараметры специализированного метода.
Предложен метод реконструкции и модификации аэродинамического профиля специализированным методом Abbott’а с применением v-кривой для аппроксимации средней линии профиля
Специализированные методы моделирования (аэро/газо/гидро)-динамических профилей используются при проектировании технических объектов во многих областях вне авиастроения. Например, при проектировании гребных винтов, лопаток ГТД, лопаток насосов, воздушных винтов энергетических установок и т.д. Описанные методики применения программы FairCurveModeler в специализированном методе моделирования аэродинамического профиля могут быть полезными и в этих областях.

Литература
1. Муфтеев В.Г. Конструирование плоских кривых методом огибающей // Изв. ВУЗов. Авиационная техника, 1980, №4, с.43-47.
2. Муфтеев В.Г., Марданов А.Р. Геометрическое моделирование кривых линий высокого качества // Прикладная геометрия. Applied Geometry [Электронный ресурс]: науч. журн. / Моск. авиационный ин-т (гос.техн.университет) "МАИ". - Электрон. журн. - Москва: МАИ, 2006. - №18; вып.8, –Режим доступа к журн.: http://www.mai.ru. – Загл. с титул.-стр. 37-66.
3. R.W. Soanes. Thrice differentiable affine conic spline interpolation. U.S. Army ARDEC Technical Report ARCCB-TR-95038, Benet Laboratories, Watervliet, NY, September 1995.
4. V.A. Osipov, V.G. Muftejev. Modelling Curvilinear Lines and Surfaces via Modified B-Splines. Computers and Industry 13 (1989) 61-67.
5. Муфтеев В.Г. Моделирование кривых высокого качества на основе v-кривых // Прикладная геометрия. Applied Geometry [Электронный ресурс]: науч. журн. / Моск. авиационный ин-т (гос.техн.университет) "МАИ". - Электрон. журн. - Москва : МАИ, 2007. - №19; вып.9 - стр. 25-74.
6. Муфтеев В.Г., Марданов А.Р., Геометрическое моделирование кривых линий и поверхностей высокого качества // Прикладная геометрия. Applied Geometry [Электронный ресурс]: науч. журн. / Моск. авиационный ин-т (гос.техн.университет) "МАИ". - Электрон. журн. - Москва : МАИ, 2006. - №18; вып.8 - стр. 67-89.
7. W.Boehm. Bezier presentation of airfoils. Computer Aided Geometric Design 4 1987 17-22. North Holland.
8. Flow Vision. Система моделирования движения жидкости и газа. Версия 2003. Руководство пользователя
9. Атлас профилей NACA.