Laboratory work. Preparation of NURBS templates of analytical curves for CAD systems

Analytical curves

Engineering problems may require analytical curves with specific properties. Such curves can be derived analytically from the solution of specific engineering problems.

A designer’s powerful reserve is a whole palette of analytical curves, the so-called, remarkable curves.

NURBS curve patterns

Currently, CAD systems use NURBS curves as analytical curve templates (as a universal internal representation of curves).

Second-order curves are reduced to NURBS curves in an exact manner.

Spatial spiral-helical lines and equidistants to flat curves are approximated to NURBS curves.

When approximating analytical curves with splines, you can use not only polylines of base points, but also the differential characteristics of analytical curves at these points. This approximation scheme is called Hermite approximation.

For geometrically stable approximation of analytical curves, the authors proposed a method of approximation by a geometric spline in the NURBzS curve format [1]. The Hermite geometric determinant is used as initial data - a reference polyline with fixed tangent and curvature vectors at the points of the base polyline.

As an example of approximation of an analytical curve, this work uses a clothoid (Cornu spiral) [2]. The clothoid has a truly remarkable property: a linear law of change in curvature along the length of the curve, starting from zero. Clothoid splines of the 2nd order of smoothness (splines composed of segments, circles and segments of a clothoid) are widely used in the design of technical objects with functional curves and surfaces.

It is also believed that the segment of an elastic bar (physical spline) between two weights from a set of weights that fix the shape of the physical spline has a linear law of change in curvature [2]. That is, it is accurately approximated by the segment of the clothoid.

The segment of the clothoid was used by the authors as a guide curve for modeling the working surface of a plow moldboard according to the diagram of Prof. Shchuchkin [3].

Building a NURBS clothoid template. Methodical instructions.

Formula of clothoid (Cornu spiral)

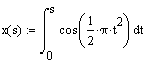
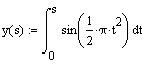
Let's prepare a section of the clothoid on the segment 0<= t <= 3

Let's calculate the first and second derivatives

Let's calculate the curvature

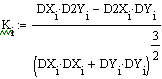
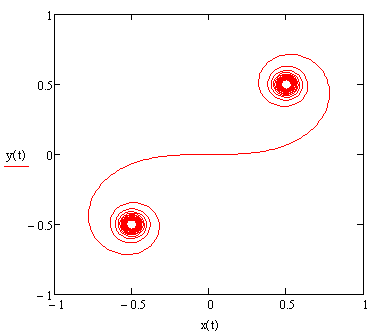
Graph of the clothoid site on the segment 0<= t <= 3

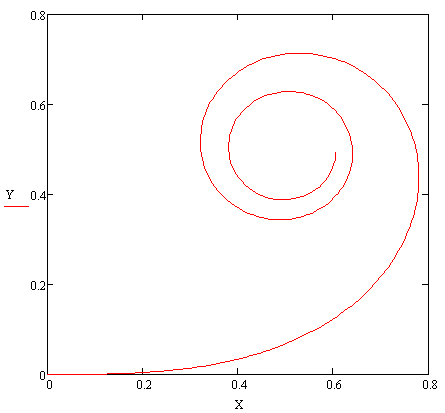
Clothoid curvature graph

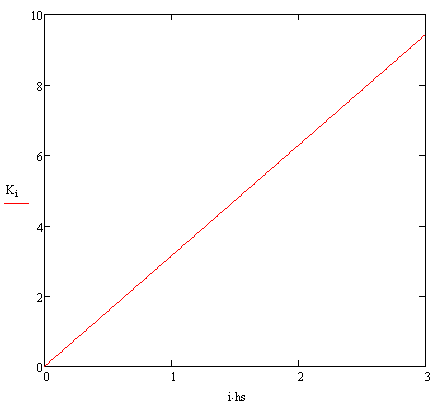
Let us introduce the curvature function squared along the length of the curve

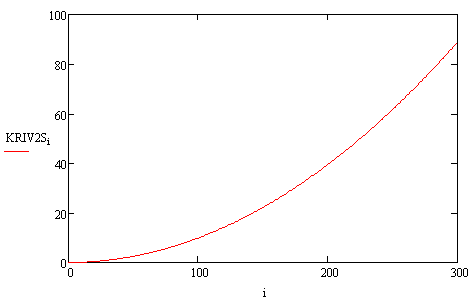
We integrate the square of curvature along the length

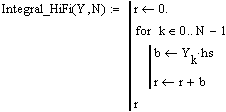
So, potential energy of the curve = 89.271

To construct a NURBzS spline using the Hermite scheme, we prepare a reference broken line of 21 points with fixed tangent vectors and curvature values

Base points

Vectors of first derivatives (tangent vectors)

Curvature

Values are specified in the X coordinate

Curvature vectors

For a plane curve, zero vectors are specified

Line graph Curvature graph

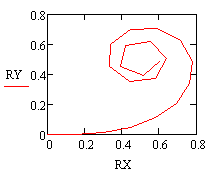
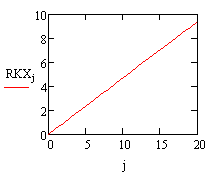
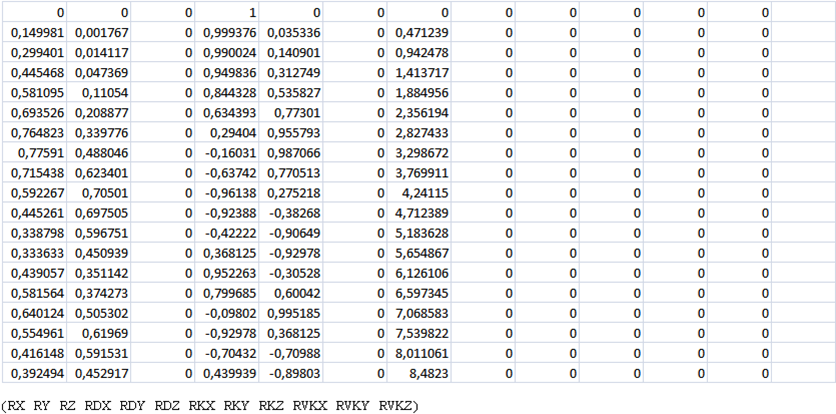
Let's prepare a table of clothoid parameters for the FairCurveModeler web application on an Excel sheet

Insert > Component > Excel > Microsoft Excel >

Create an Empty Excel worksheet > Inputs - set to 12 > Outputs - set to 0 > In the placeholders, enter the variables

RX, RY, RZ, RDX, RDY, RDZ, RKX, RKY, RKZ, RVKX, RVKY, RVKZ

Double click on the table.

Select the area with parameters on the Excel sheet that appears. Click PC mouse on sheet

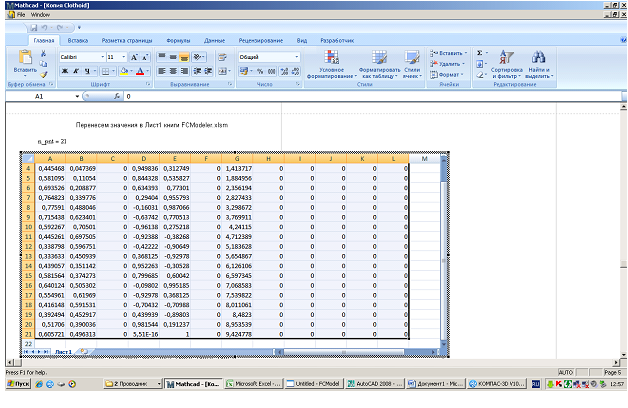
In the context menu, click Copy and then Copy

Transfer the Excel table with parameters to AutoCAD / ZWCAD using the standard commands of these systems and run the V_Hermite command.

Bibliography

1. Mufteev V.G. High quality curve modeling based on the v-curve method. Applied geometry. Applied Geometry [Electronic resource]: scientific. magazine / Moscow Aviation Institute (State Technical University) "MAI". - Electron. magazine - Moscow: MAI, 2007. - No. 19; issue 9, -page 25-74. - Access mode to the journal: http://www.mai.ru. - Cap. with title. screen. - State registration number 019164.

2. Fox A., Pratt M. Computational geometry. Application in design and production / Transl. from English M.: Mir, 1982. -304 s.

3. Mudarisov S.G., Mufteev V.G., Farkhutdinov I.M. Geometric modeling of dynamic surfaces of working bodies of agricultural machines. Materials of the All-Russian Scientific and Practical. Conf. "Current problems of the agro-industrial complex", dedicated to. 65th anniversary of the Ulyanovsk State Agricultural Academy and 20th anniversary of the Department of Life Safety and Energy February 6-8, 2008 - Ulyanovsk. pp. 136-143.